Движение жидкости в пласте с неоднородной проницаемостью

Проницаемость в различных точках продуктивных пластов не является строго постоянной величиной. Иногда изменение проницаемости по пласту носит столь хаотичный характер, что пласт можно рассматривать в среднем однородно проницаемым.

Если изменение проницаемости носит не случайный характер, а на значительном протяжении пласта имеет место определенные закономерности в изменении проницаемости, тогда движение жидкостей и газов существенно отличается от движения их в однородных пластах.

Отметим следующие простейшие случаи неоднородности пластов.

1.Пласт состоит из нескольких слоев (рис.4.14, 4.15, стр. 191).

В пределах каждого слоя проницаемость в среднем одинакова и скачкообразно изменяется при переходе от одного слоя к другому. Допустим, что все n слоев горизонтальный, мощность i-го слоя h₁, проницаемость соответствующего слоя k₁. На одном конце каждого слоя давление равно р_к, на другом – р_r.

Если движение жидкости прямолинейно – параллельное (см. рис. 4.14) по закону Дарси, то распределение давление р в каждом слое линейное и характеризуется уравнением

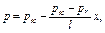(4.63)

дебит потока вычисляется по формуле

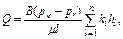(4.64)

а средний коэффициент проницаемости по формуле

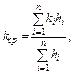(4.65)

В случае плоскорадиального движения жидкости в многослойном пласте к гидродинамически совершенной скважине по закону Дарси (см. рис. 4.15) давление в каждом слое меняется по логарифмическому закону

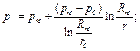(4.66)

дебит скважины определяется по формуле

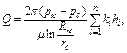(4.67)

а средний коэффициент проницаемости пласта и в этом случае находится по (4.65).

2.Пласт состоит из нескольких зон различной проницаемости (рис. 4.16, 4.17, стр. 192)

На границе двух зон проницаемость меняется скачкообразно, а в пределах одной и той же зоны проницаемость в среднем одинакова. С неоднородностью такого рода можно встретиться, например, при соприкосновении двух разных пластов вдоль сброса или в случае наличия порога фациальной изменчивости одного и того же пласта.

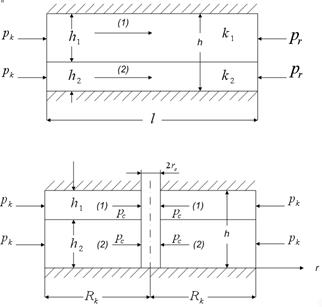
Рис. 4.14, 4.15. Многослойный пласт

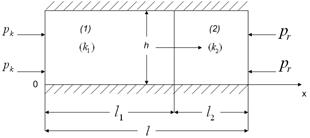
Рис. 4.16. Пласт с зонами различной проницаемости

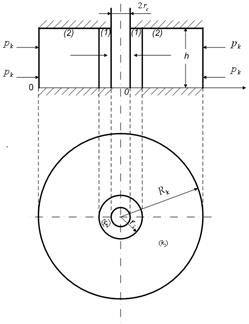
Рис. 4.17. Зоны кольцеобразной формы

Допустим, что горизонтальный пласт мощностью h, длиной l с непроницаемыми кровлей и подошвой состоит из n зон различной проницаемости, длина i-той зоны l_i, коэффициент проницаемости k_i (cм. рис. 4.16).

При прямолинейно – параллельной фильтрации жидкости в таком пласте по закону Дарси дебит фильтрационного потока рассчитывается по формуле

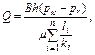(4.66)

где В – ширина потока.

Средний коэффициент проницаемости

(4.67)

При n=2 распределение давления в первой зоне р₁ и во второй – р₂ описывается уравнениями:

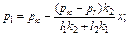
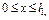(4.68)

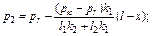
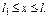
Если при плоскорадиальном притоке жидкости к гидродинамически совершенной скважине по закону Дарси зоны различной проницаемости пласта имеют кольцеобразную форму (см. рис. 4.17), то формула дебита скважины имеет вид:

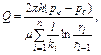(4.69)

где k₁- коэффициент проницаемости зоны за номером i; r_i-1 и r₁ – соответственно внутренний и внешний радиусы этой зоны, причём r₀=r₀, a r_n = R_k.

Средний коэффициент проницаемости в этом случае находится по формуле

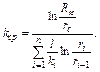
При n=2 распределение давления в первой зоне р₁ и во второй зоне р₂ определяется по формулам

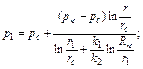
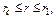(4.70)

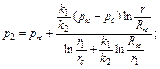
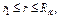
3.Проницаемость пласта непрерывно изменяется, увеличиваясь или уменьшаясь в определенном направлении.

Допустим, что при плоскорадиальном течении коэффициент проницаемости изменяется по линейному закону

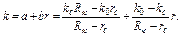
У забоя скважины коэффициент проницаемости равен k_c, а на контуре питания (r=R_x) k=k₀. Фильтрация жидкости происходит по закону Дарси. В этом случае формула для дебита имеет вид:

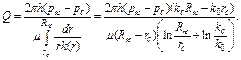(4.71)