Спосіб заміни стержнів

При визначенні зусиль у складних фермах, як правило, доводиться розв’язувати системи рівнянь. Але в деяких випадках складну ферму можна перетворити в найпростішу або в систему, при розрахунку якої не потрібно спільного розв’язання рівнянь. Для цього у вихідній системі видаляються певні стержні й уводяться інші – замінюючі. Так як в заданій замінюючій системі стержнів немає, то для визначення зусиль можна скласти додаткові рівняння, що виражають рівність нулю зусиль у кожному замінюючому стержні. Такий спосіб розрахунку називається способом заміни стержнів.

Розглянемо складну ферму (рис.3.8,а). При використанні для визначення зусиль у стержнях такої ферми способу моментної точки або способу проекцій приводить до розв’язання системи рівнянь.

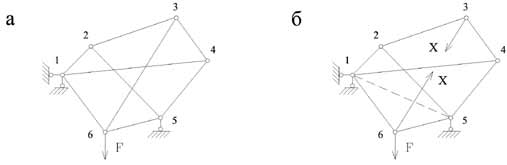
Рис.3.8

Замінимо стержень 6-3 стержнем 1-5. Така заміна перетворить ферму в найпростішу й не являється єдино можливою. Легко переконатися, що отримана система (рис.3.8,б) є геометрично незмінною.

Для визначення зусиль у перетвореній системі можна використовувати один з розглянутих раніше способів, наприклад, спосіб вирізання вузлів. Якщо сили Х у замінюючому стержні 3-6 підібрати так, що зусилля в замінюючому стержні 1-5 буде дорівнює нулю, то обидві системи (рис.3.8,а,б) будуть еквівалентні, а зусилля в їхніх відповідних стержнях – однаковими.

На підставі принципу незалежності дії сил зусилля в будь-якому i-ому елементі (як заданої, так і перетвореної системи) може бути знайдене по формулі

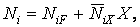
де 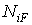– зусилля в перетвореній системі від заданого навантаження, 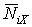– зусилля від одиничної сили .

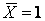Обчислене по цій формулі зусилля 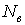в замінюючому стержні повинне дорівнювати нулю, тому що в заданій системі цього стержня немає:

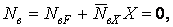
звідки

.

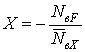По формулі (3.1) з врахуванням (3.2) можна визначити зусилля в усіх елементах системи.

В більш складних випадках виконується заміна двох і більше стержнів, що приводить до розв’язання системи рівнянь:

(3.3)

де 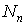– зусилля в n-ому з стержні 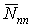, - зусилля в n-ому замінюючому стрижні від сили .

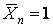Положення амінюючого стержня можна знайти з наступних міркувань. Видаливши який-небудь стержень із заданої ферми, потрібно потім послідовно відкидати в ній вузли, приєднані двома стержнями, що не впливає на геометричну незмінюваність залишеної частини ферми. В кінці знайдеться стержень, що не має необхідного для геометричної незмінюваності зв'язку. Стержень, що забезпечує цей зв'язок і буде замінюючим. Якщо отримана ферма не буде найпростішою, то з неї потрібно видалити ще один стержень і відкидати вузли, приєднані двома стержнями, доти, поки знову не виявиться стержень, що не має достатнього зв'язку із залишеною частиною ферми, що визначить положення другого замінюючого стержня і так далі.