Визначення зусиль за допомогою ліній впливу

Будемо розглядати два види навантаження системи: 1) зосередженими силами; 2) рівномірно розподіленими навантаженнями.

Дія зосереджених сил.

Для визначення якого-небудь зусилля від дії однієї сили 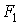потрібно виміряти під точкою прикладення сили ординату лінії впливу цього зусилля й помножити її на величину сили. При одночасній дії системи зосереджених сил на підставі принципу незалежності дії сил потрібно те ж саме виконати для кожної сили й отримані результати скласти.

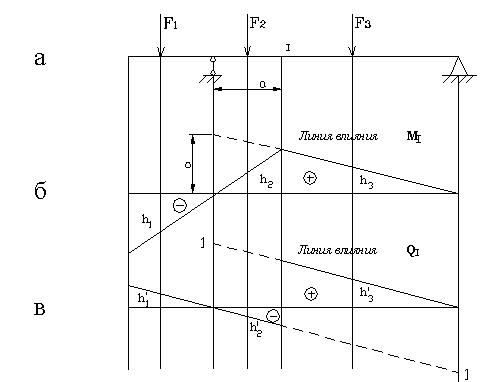
Рис.2.9

Наприклад, для визначення згинального моменту в перетині 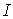(рис.2.9,б) потрібно сили 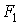, , 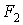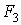помножити на розташовані під ними ординати лінії впливу 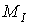(з урахуванням знаків цих ординат) і тоді:

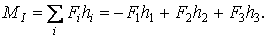
Аналогічним чином обчислюється й поперечна сила в перетині 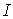(рис.2.9,б):

.

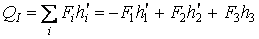Дія рівномірно розподілених навантажень.

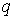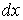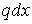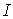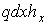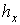Нехай на деякій ділянці балки (рис.2.10,а) прикладене рівномірно розподілене навантаження інтенсивністю . Замінимо на нескінченно малій ділянці розподілене навантаження зосередженою силою . Від цієї зосередженої сили згинальний момент у перетині дорівнює , де — ордината лінії впливу 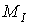під силою (рис.2.10,б). Все розподілене навантаження можна представити як нескінченно велика кількість зосереджених сил 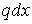. Згинальний момент у перетині 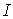від такої системи сил буде дорівнює сумі всіх добутків :

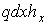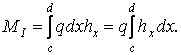
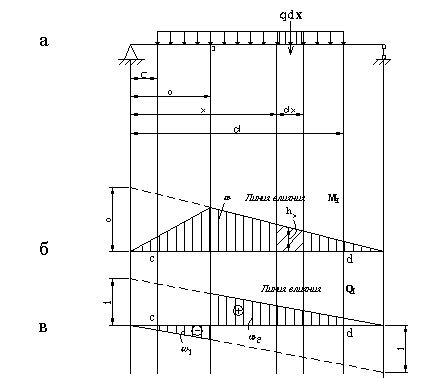
Рис.2.10

Вираз, що стоїть під знаком інтеграла, являє собою елементарну площадку лінії впливу 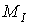на ділянці 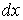(похиле штрихування на рис.2.10,б), а інтеграл, обчислений у межах від 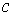до 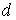дорівнює площі лінії впливу 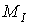на ділянці від 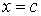до 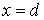(вертикальне штрихування на рис.2.10,б). Якщо цю площу позначити через 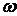, то:

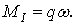
Таким чином, для визначення зусилля від рівномірно розподіленого навантаження потрібно інтенсивність цього навантаження помножити на площу лінії впливу в межах розташування навантаження.

Якщо під розподіленим навантаженням лінія впливу має різні знаки, то площі окремих ділянок беруться з урахуванням знаків лінії впливу, так, поперечна сила в перетині 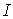(рис.2.10,в) визначається у вигляді: