Приклади кінематичного аналізу

Приклад 1. Виконати кінематичний аналіз системи (рис.1.10,а).

Визначаємо ступінь свободи системи по формулі П.Л.Чебишева:

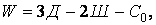
(1.3)

де Д – число дисків, Ш – число простих шарнірів, С₀ – кількість стержнів.

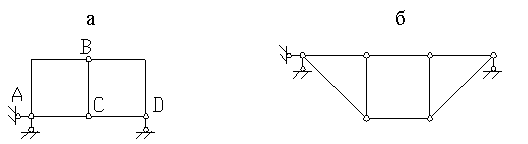
Рис.1.10

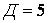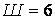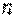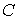Відкидаючи всі шарніри й опорні стержні, знаходимо, що система складається з п'яти дисків ( ). Відкидаючи опорні стержні, визначаємо число шарнірів, приведених до простих ( : по двох у точках і , по одному – у точках 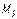і 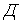). Число опорних стержнів – .

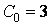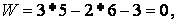
тобто система може бути геометрично незмінною й статично невизначеною. Щоб переконатися, що це так, виконаємо аналіз структури системи. Тому що диски , і 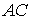зв'язані трьома шарнірами 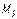, 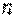і 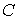, що не лежать на одній прямій, то вони утворять диск, до якого жорстко приєднаний диск 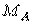за допомогою шарніра 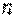й стержня 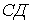, вісь якого не проходить через центр шарніра. Ця незмінна фігура жорстко приєднана до землі за допомогою трьох стержнів, що не перетинаються в одній точці. Таким чином, система (рис.1.10,а) геометрично незмінна й не є миттєво змінюваною.

Приклад 2. Виконати кінематичний аналіз системи (рис.1.10,б).

Тому що система є шарнірно-стержневою, то для визначення її ступеня свободи використовуємо формулу

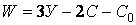
(1.4)

де 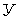– число вузлів ферми; 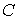– число внутрішніх стержнів; 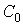– число опорних стержнів.

Тут 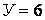, , 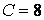, 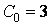отже,

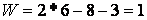
Таким чином, система має один ступінь свободи, є механізмом і не може використовуватися як будівельна конструкція.

Приклад 3. Дослідити систему (рис.1.11,а).

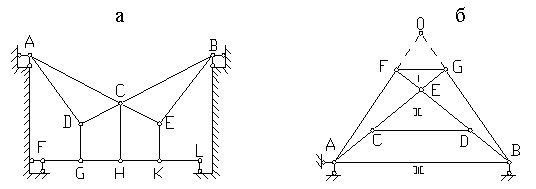
Рис.1.11

Ступінь свободи системи визначимо по формулі (1.3):

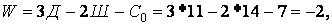
Отже, система має два зайві зв'язки. Щоб переконатися в її геометричній незмінюваності, проаналізуємо структуру системи. Тут можна виділити два незмінних трикутник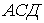и й 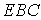, які жорстко з'єднані один з одним і з землею (розглянутою як диск) за допомогою трьох шарнірів 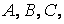не лежачих на одній прямій. Стержень 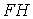прикріплений до цієї незмінної частини системи за допомогою шарніра 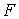й стержня 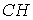, що не проходить через центр шарніра, так само як і стержень 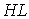за допомогою шарніра 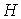й опорного стержня 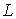. Стержні 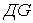й 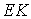– зайві, тому що й без них система незмінна.

Приклад 4. Виконати кінематичний аналіз системи (рис.1.11,б).

Використовуючи формулу (1.4), визначаємо число ступенів свободи системи:

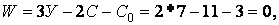
отже, система має необхідну кількість зв'язків, щоб бути геометрично незмінною й статично визначеною.

Проаналізуємо структуру. Виділимо незмінні трикутник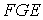и й 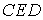. Стержень 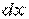становить єдине ціле із землею (третій диск), тому що прикріплюється трьома опорними стержнями, що не перетинаються в одній точці. Щоб перевірити, чи жорстко з'єднані диски І, ІІ, ІІІ (рис.1.11,б), переконаємося, що три їхніх миттєвих центри обертання не лежать на одній прямій. Шарнір 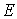є миттєвим центром обертання дисків І й ІІ, а також дисків ІІ й ІІІ, тому що тут перебуває фіктивний шарнір, що заміняє стержні 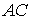й 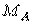, що з'єднують ці два диски. Отже, система миттєво змінювана, тому що де б не перебував миттєвий центр обертання О дисків І й ІІІ, через нього й точку 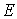завжди можна провести пряму, на якій будуть лежати всі три миттєвих центри обертання.

Приклад 5.Дослідити ферму (рис.1.12).

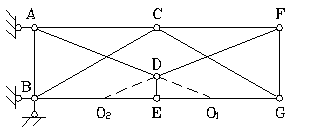
Рис.1.12

По формулі (1.4) визначаємо ступінь свободи ферми:

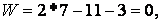
отже, система може бути геометрично змінюваною й статично визначеною.

Проаналізуємо систему. Вона складається із трьох дисків – трикутники 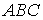, 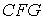і стержень 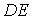,- зв'язаних між собою стержнями 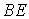, , 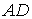, , 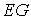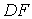які можна замінити фіктивними шарнірами 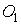, 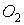і шарніром 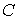. Отже, можна зробити висновок: всі стержні з'єднані між собою жорстко й прикріплюються до землі так само жорстко за допомогою трьох стержнів, що не перетинаються в одній точці.

Для перевірки системи на миттєву змінюваність застосуємо спосіб нульового навантаження – визначимо опорні реакції й зусилля у всіх стержнях за умови, що зовнішнього навантаження немає. З умов рівноваги всієї системи ( 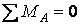; ; 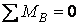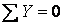) знаходимо, що опорні реакції дорівнюють нулю. Вирізуючи вузол 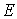і проектуючи всі сили на вертикаль, знаходимо, що зусилля у вертикальному стержні 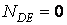. Потім, записуючи рівняння проекцій двох сил, що сходяться у вузлі 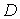(третя сила 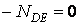), на напрямки нормалей до цих стержнів, знаходимо, що зусилля в стержнях 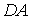і 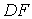також дорівнюють нулю. Нарешті, розглядаючи рівновагу вузлів 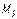, , 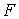, , 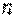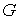знаходимо, що зусилля у всіх стержнях системи при відсутності навантаження дорівнюють нулю, отже, система незмінна.

Приклад 6. Виконати кінематичний аналіз системи (рис.1.13,а).

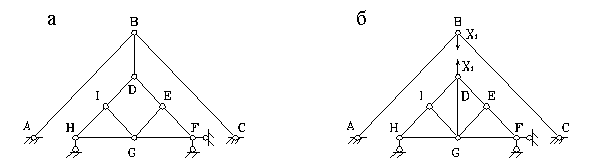
Рис.1.13

По формулі (1.4) визначаємо ступінь свободи:

тобто система має необхідний мінімум зв'язків, щоб бути геометрично незмінною. Для перевірки того, чи є система дійсно незмінною, використовуємо метод заміни стержнів. Виберемо замінюючу систему (рис.1.13,б). Тут відкинутий стержень , а його дія замінена силами 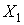, і доданий замінюючий стержень 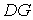. Обрана замінююча система, незмінна: стержні 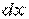, 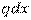і земля жорстко з'єднані трьома шарнірами, що не лежать на одній прямій. А нижня частина системи незмінна, оскільки складається із трикутника (наприклад, 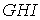), до якого жорстко прикріплені всі інші вузли за допомогою діад, і все це прикріплено до землі трьома опорними стержнями.

Тепер визначимо зусилля в замінюючому стержні від сил 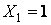. Вирізуючи послідовно вузли 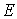, , 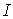і розглядаючи їхню рівновагу, одержимо, що зусилля в замінюючому стержні дорівнює нулю, отже, вихідна система - миттєво змінювана.

Балки