Статична визначеність геометрично незмінних стержневих систем

Спорудження статично визначене щодо опорних закріплень тільки в тому випадку, коли число параметрів, що визначають реакції цих закріплень, дорівнює трьом. Цій умові задовольняють наступні три системи опорних закріплень:

1. Комбінація шарнірно-рухомої й шарнірно-нерухомої опор (рис.1.8,а);

2. Комбінація трьох шарнірно-рухомих опор (рис.1.8,б) за умови, що напрямки реакцій цих опор не перетинаються в одній точці й не паралельні один одному;

1. Жорстко затиснена система (рис.1.8,в).

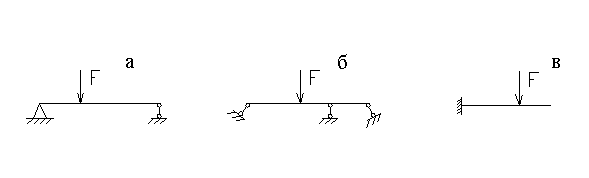
Рис.1.8

Наявність у геометрично незмінної системи чотирьох і більше опорних стержнів, серед яких є три стержні з напрямками реакцій, що не перетинаються в одній точці й не паралельними один одному, говорить про те, що спорудження статично невизначене.

Розглянемо умови, яким повинні задовольняти самі статично визначені стержневі системи (ферми), тобто такі системи, зусилля в елементах яких можуть бути знайдені за допомогою одних лише рівнянь статики.

При дії на шарнірну ферму зосереджених сил, прикладених у вузлах, у її прямолінійних стержнях виникають тільки повздовжні (стискаючі або розтягуючі) сили. Якщо ферма має криволінійні стержні, то в поперечних перерізах цих стержнів крім повздовжніх сил виникають і згинальні моменти, що викликають у них додаткові напруги.

Якщо ферма в цілому (рис.1.9,а) перебуває в рівновазі під дією сил, прикладених до її вузлів, то й будь-який її вузол (рис.1.9,б) також перебуває в рівновазі, тобто зовнішнє навантаження, що діє на вузол, і внутрішні зусилля в стержнях, що сходяться в цьому вузлі, взаємно врівноважуються.

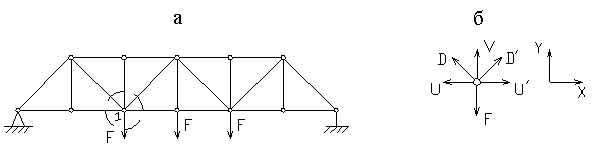
Рис.1.9

На кожний вузол ферми діє система сил, що перетинаються в одній точці. Для такої системи сил можна записати два рівняння рівноваги:

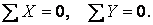
Якщо ферма має 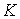вузлів, то для них можна записати 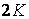рівнянь рівноваги, з яких можна визначити зусилля у всіх стержнях ферми й три невідомі опорні реакції. Будь-які інші рівняння рівноваги для окремих частин ферми або для всієї ферми в цілому можуть бути отримані із цих рівнянь, тому вони не є новими незалежними умовами для визначення незалежних зусиль. Таким чином, ферма буде статично визначена, якщо число її стержнів 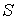дорівнює подвоєному числу вузлів мінус 3:

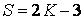
(1.2)

Залежність (1.2) між числом вузлів і числом стержнів статично визначеної ферми збігається з умовою (1.1) її геометричної незмінюваності.

Отже, усяка найпростіша ферма, тобто ферма, утворена на базі шарнірного трикутника послідовним приєднанням вузлів (кожного за допомогою двох стержнів, що не лежать на одній прямій), є одночасно геометрично незмінною й статично визначеною системою.

Всі стержні статично визначеної системи є безумовно необхідними з погляду геометричної незмінюваності, тобто в такій системі немає ні одного зайвого зв'язку; якщо ж число стержнів геометрично незмінної системи перевищує мінімально необхідне, то вона є статично невизначеною.