Кривые второго порядка

Уравнение 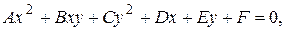если А, В и С одновременно не равны нулю, задает на плоскости линию, которую называют кривой второго порядка.

Если В=0 кривая имеет ось симметрии параллельную координатным осям. Будем рассматривать только этот случай.

Выделяя полный квадрат относительно каждой переменной x и y, уравнение 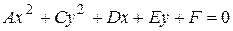приводим к одному из следующих канонических видов:

1. 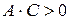– линии эллиптического типа:

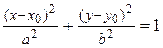– эллипс с центром 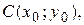полуосями а и b.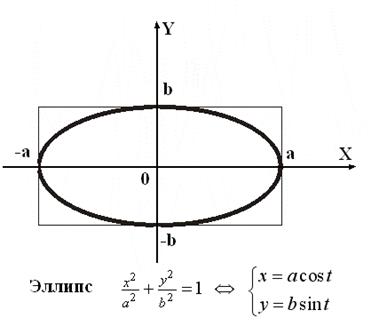

Если 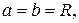то уравнение запишется в виде

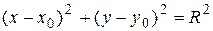
– окружность с центром 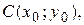радиуса R.

2. 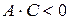– линии гиперболического типа:

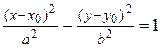– гипербола с центром 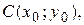вещественной полуосью – а, мнимой полуосью – b.

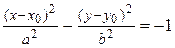– сопряженная гипербола с центром 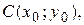вещественной полуосью – b, мнимой полуосью – а.

3. 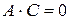– линии параболического типа.

Здесь возможны четыре случая:

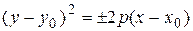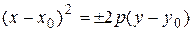либо – параболы с вершиной 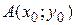, где .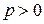

В первом случае – ось симметрии параллельна оси 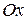, во втором –

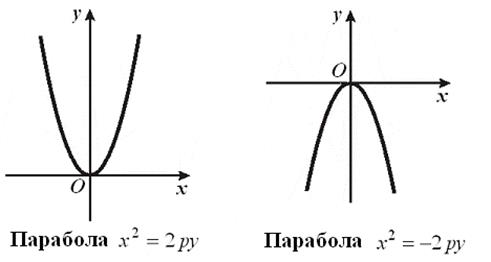
Если в уравнении знак “+”, ветви параболы направлены в положительном направлении оси симметрии, знак “–” — в противоположном.

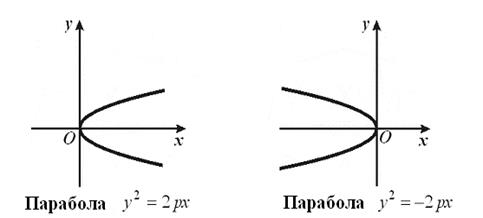
Замечание. Возможны так называемые вырожденные случаи:

1) :

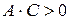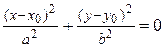– точка .

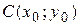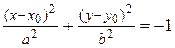– мнимый эллипс.

2) 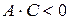: 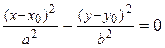или

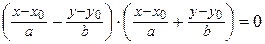
– пара пересекающихся прямых: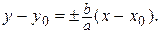

3) 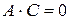: 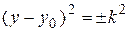или 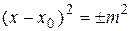– пара мнимых прямых, пара параллельных прямых.

4. ВЕКТОРНАЯ АЛГЕБРА

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ