Элементы линейной алгебры
Темы рефератов:
1. История открытия возбудителя холеры.
2. История пандемий холеры.
3. Особенности биологии возбудителя холеры на современном этапе.
4. История открытия возбудителя хеликобактерной инфекции.
5. Роль H. pylori в развитии рака желудка.
6. Значение H. fennelli, H. cinaedi. в инфекционной патологии человека.
8. Рекомендованная литература по теме занятия:
Обязательная:
1. Поздеев, О. К. Медицинская микробиология: учеб. пособие / О.К. Поздеев – М.: ГЭОТАР-Медиа,2008. – 768 с.
Дополнительная:
1. Ярилин, А.А. Иммунология: учебник / А.А. Ярилин – М.: ГЭОТАР-Медиа, 2010. – 752 с.
2. Гиллеспи, С.Х. Наглядные инфекционные болезни и микробиология / С.Х. Гиллеспи, К.Б. Бамфорд – М.: ГЭОТАР-Медиа, 2009. – 136 с.
3. Хаитов, Р.М. Иммунология: учебник / Р.М. Хаитов – М.: ГЭОТАР-Медиа, 2011. – 528 с.
4. Медицинская микробиология, вирусология и иммунология: 1 т.: учебник / ред. В.В. Зверев [и др.] – М.: ГЭОТАР-Медиа, 2010.- 448 с.
5. Медицинская микробиология, вирусология и иммунология: 2 т.: учебник / ред. В.В. Зверев [и др.] – М.: ГЭОТАР-Медиа, 2010.- 477 с.
Аналитическая геометрия. Комплексные числа
Элементы линейной алгебры
1. 1. Матрица. Основные понятия. Матрицей А размера 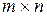 называется множество
называется множество 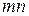 элементов расположенных в виде прямоугольной таблицы из
элементов расположенных в виде прямоугольной таблицы из 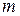 строк и
строк и 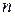 столбцов, имеющей вид:
столбцов, имеющей вид:
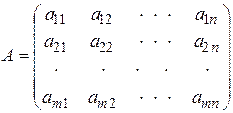 .
.
Если 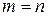 , то А называется квадратной матрицей. Квадратные матрицы размера
, то А называется квадратной матрицей. Квадратные матрицы размера 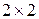 и
и 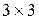 называются матрицами второго и третьего порядка, соответственно.
называются матрицами второго и третьего порядка, соответственно.
Квадратная матрица, элементы главной диагонали которой единицы, а все остальные элементы нули, называется единичной:
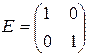 ,
, 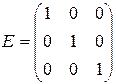 .
.
Матрица вида  называется матрицей–столбцом.
называется матрицей–столбцом.
Пусть даны две матрицы:
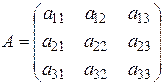 ,
, 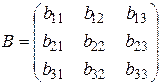 .
.
1) Суммой (разностью) матриц А и В называется матрица, элементы которой равны сумме (разности) соответствующих элементов матриц
А и В:
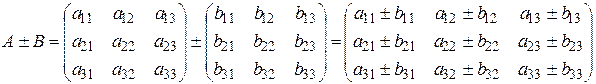 .
.
2) Умножение матрицы на число. При умножении матрицы А на число 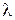 , на это число умножаются все элементы матрицы:
, на это число умножаются все элементы матрицы:
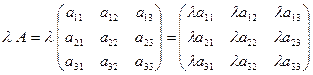 .
.
3) Произведение матрицы А на матрицу В обозначается символом АВ и определяется равенством:
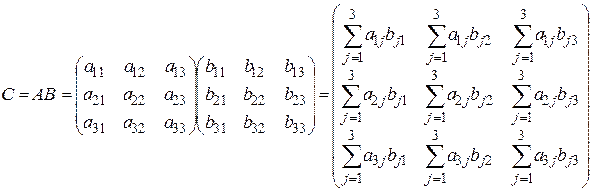 .
.
т. е. элемент матрицы произведения, стоящий в 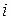 -й строке и
-й строке и 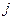 -м столбце, равен сумме произведений соответственных элементов
-м столбце, равен сумме произведений соответственных элементов 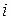 -й строки матрицы А и
-й строки матрицы А и 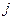 -го столбца матрицы
-го столбца матрицы 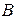 . Например.
. Например.
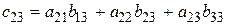 .
.
Необходимо знать, что 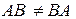 (в общем случае), но в некоторых случаях равенство может иметь место. Например:
(в общем случае), но в некоторых случаях равенство может иметь место. Например: 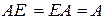 .
.
1. 2. Определитель. Определителем второго порядка, соответствующим матрице 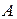 называется число, вычисляемое по формуле:
называется число, вычисляемое по формуле:
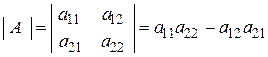 .
.
Аналогично, определителем третьего порядка называется число, определяющееся равенством:
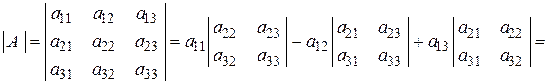
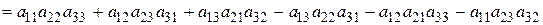 .
.
Минором 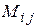 элемента
элемента 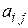 определителя третьего порядка называется определитель второго порядка, который получится, если в исходном определителе вычеркнуть строку и столбец, содержащий данный элемент. Алгебраическим дополнением
определителя третьего порядка называется определитель второго порядка, который получится, если в исходном определителе вычеркнуть строку и столбец, содержащий данный элемент. Алгебраическим дополнением 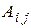 элемента
элемента 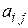 называется произведение его минора на
называется произведение его минора на 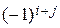 , где
, где 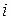 и
и 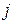 номера строки и столбца, содержащих данный элемент. Например:
номера строки и столбца, содержащих данный элемент. Например:
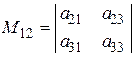 , тогда
, тогда 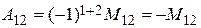 .
.
Пример 1. Даны матрицы
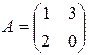 ;
; 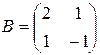 ;
; 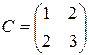
Найти матрицу 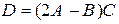 и вычислить ее определитель.
и вычислить ее определитель.
Решение.
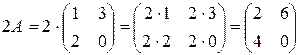 ,
,
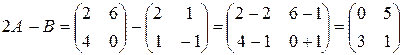 ,
,
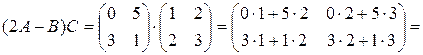
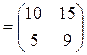 ,
,
т. е. 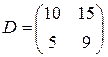
 .
.
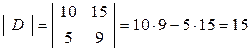 .
.
Дата добавления: 2015-01-29; просмотров: 1149;
