Прямая линия
Общее уравнение прямой
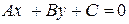 .
.
Две прямые 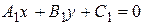 и
и 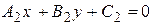 параллельны, если
параллельны, если 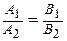 , перпендикулярны, если
, перпендикулярны, если 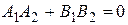 . Расстояние от точки
. Расстояние от точки 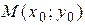 до прямой
до прямой 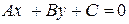 вычисляется по формуле:
вычисляется по формуле:
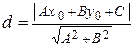 .
.
Уравнение прямой с угловым коэффициентом:
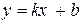 .
.
Угол 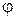 , отсчитанный против часовой стрелки от прямой
, отсчитанный против часовой стрелки от прямой 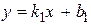 , до прямой
, до прямой 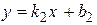 определяется формулой:
определяется формулой:
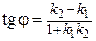 .
.
Условие параллельности двух прямых: 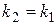 ,
,
Условие перпендикулярности : 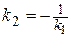 .
.
Уравнение прямой, проходящей через данную точку 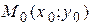 , или уравнение пучка прямых:
, или уравнение пучка прямых:
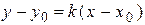 .
.
Уравнение прямой, проходящей через две данные точки 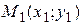 и
и 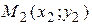 :
:
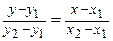 .
.
Угловой коэффициент прямой, проходящей через две точки: 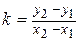 .
.
Уравнение прямой в отрезках на осях: 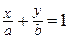 .
.
Пример 1. Через точку 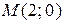 провести прямые параллельно, перпендикулярно и под углом
провести прямые параллельно, перпендикулярно и под углом 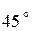 к прямой (АВ):
к прямой (АВ):  .
.
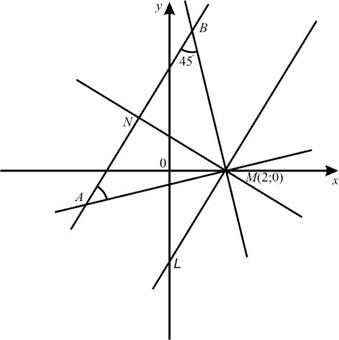
Решение. Уравнения прямых, проходящих через точку 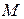 :
:
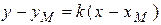 ,
,
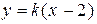 .
.
Найдем угловые коэффициенты искомых прямых. Прямая (АВ) задана общим уравнением:  . Выразив из него
. Выразив из него 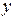 , получаем уравнение с угловым коэффициентом
, получаем уравнение с угловым коэффициентом 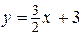 ;
; 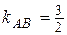 .
.
1.  .
.
Уравнение 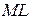 :
: 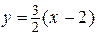 или
или 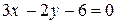 .
.
2. 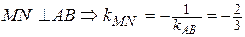 .
.
Уравнение 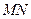 :
: 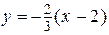 или
или 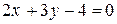 .
.
3. Прямая 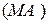 образует с
образует с 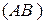 угол
угол 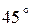 . Обозначим ее угловой коэффициент через
. Обозначим ее угловой коэффициент через 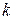 и воспользуемся формулой
и воспользуемся формулой
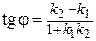
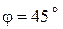 ;
; 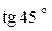 =1. Имеем
=1. Имеем 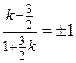 , так как искомое
, так как искомое 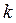 может совпадать с
может совпадать с 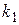 или
или 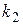 .
.
1) 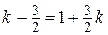 ;
;  ;
; 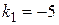 .
.
2) 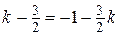 ;
; 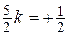 ;
; 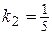 .
.
Искомые прямые
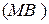 :
: 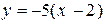 или
или 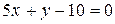 .
.
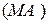 :
: 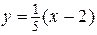 или
или 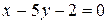 .
.
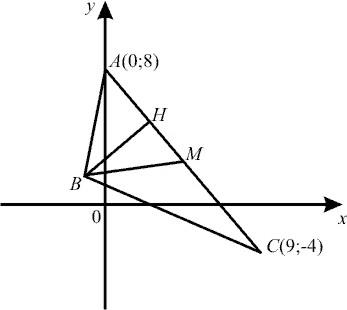 Пример 2.
Пример 2. 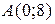 ;
;  ;
; 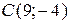 вершины треугольника. Найти уравнения стороны АС, высоты, медианы, проведенных из вершины В, длину этой высоты, угол А.
вершины треугольника. Найти уравнения стороны АС, высоты, медианы, проведенных из вершины В, длину этой высоты, угол А.
Решение. 1)Прямая (АС) проходит через две точки
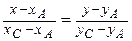 ;
; 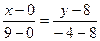 ;
;
(АС): 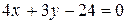 или
или 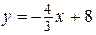 ;
; 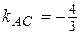 .
.
2) 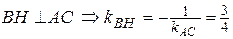
(ВН): 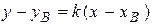 ;
; 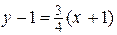 ;
; 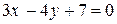 .
.
3) ВМ – медиана, М – середина АС,
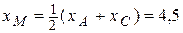 ;
; 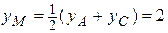 ;
;
(ВМ): 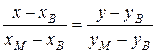 ;
; 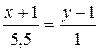 ;
;  .
.
4) Длина высоты 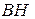 равна расстоянию от точки В до прямой АС
равна расстоянию от точки В до прямой АС
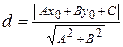 ;
; 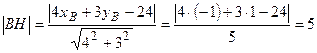 (ед.).
(ед.).
5) 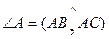 ;
; 
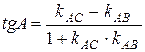 ;
;
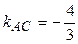 ;
; 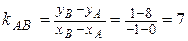 .
.
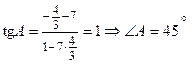 .
.
Дата добавления: 2015-01-29; просмотров: 854;
