Бюджетные возможности и бюджетная линия

Обратимся теперь ко второму главному фактору, определяющему поведение потребителя, а именно к ограниченности имеющихся в его распоряжении денежных средств.

Рассмотренное нами при анализе кардинализма уравнение (5.3):

Q_х P_x + … +Q_у P_y = i,

сохраняет свою справедливость и в рамках ординалистского подхода. В самом деле, его суть состоит в фиксации очевидного факта, что величина расходов (бюджета) потребителя равна количеству приобретенных им товаров, помноженных на их цены. Этот показатель совершенно не затрагивает проблему измеримости или неизмеримости полезностей, разделяющую между собой два названных теоретических подхода.

На рис. бюджетные возможности имеют вид бюджетной линии и соответствуют личному денежному доходу потребителя, который при данных рыночных ценах используется на приобретение потребительских благ. Любая точка на бюджетной линии ¾ это выбор из вариантов товарных наборов, между которыми потребитель распределил свой денежный доход, личный бюджет.

Или по-другому: любая точка на бюджетной линии отражает максимальный объем товаров, который при данном уровне цен потребитель может приобрести в рамках своего бюджета. Разные точки бюджетной линии отражают разные комбинации этих товаров. Но во всех случаях доход израсходован полностью. И увеличить закупки какого-либо блага без сокращения закупок другого невозможно.

Простейший случай бюджетной линии для двух товаров (X и Y) представлен на рис. 5.5.

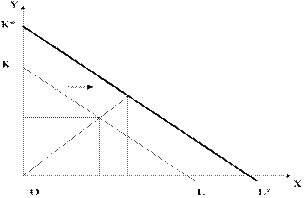
Рис. 5.5. Бюджетная линия потребителя

Легко видеть, что бюджетная линия KL является прямой. В самом деле, если выразить из уравнения (5.3) объем закупки любого из двух товаров при неизменном размере бюджета потребителя, соответствующая формула будет иметь вид линейного уравнения.

Что касается угла наклона бюджетной линии, то он определяется отношением цены за единицу Х-блага к цене за единицу Y-блага.

Обратим внимание и на треугольник КОL. Любая точка внутри него соответствует набору товаров в количественном отношении меньшему, чем наборы товаров, лежащие на прямой KL. Поэтому все данные наборы могут быть куплены с неполным использованием средств, имеющихся в распоряжении потребителя.