ПРЕДМЕТ І ЗАВДАННЯ ІСТОРІЇ ПЕДАГОГІКИ 2 страница
Имеется еще целый ряд числовых характеристик СВ, однако в теории надежности они используются редко.
Законы распределения случайных величин
Закон распределения вероятностей получения значений случайных величин в процессе эксперимента – это любое соотношение между случайными величинами и вероятностями их появления. Закон распределения бывает нескольких форм:
1) числовой ряд – получается в процессе проведения эксперимента. В этом случае закон распределения для практического применения не годится. Это – «сырье», которое дает результат при дальнейшей обработке, исходный статистический материал.
2) вариационный ряд – это то же самое, только значения в нем упорядочены.
3) таблица – каждой величине соответствует вероятность ее появления:
| Случайная величина Xi | X1 | X2 | X3 | … | Xn |
| Вероятность ее появления | p1 | P2 | p3 | … | Pn |
В таком виде представить зависимость неудобно, поэтому иногда пользуются укрупненными графиками.
 |
Часто на основании многоугольника распределения строят гистограмму. Для многих исследований гистограммы являются результатом.
4) график – используется, когда имеется много статистического материала.
 |
Функция распределения вероятностей значений случайной величины – это вероятность того, что случайная величина примет значение, меньшее некоторого фиксированного, наперед заданного, числа.
X1, X2,…,Xn – генеральная совокупность;
R – некоторое число.
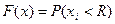 |
Графически функция распределения F(x) – это вероятность того, что случайная величина Xi займет точку левее R:
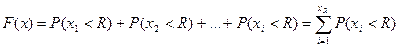 |
F(x) принимает столько значений, сколько реализаций имеет случайная величина.
xR – последнее значение xi, меньшее R.
Рассмотрим график F(x) для дискретных СВ. Пусть имеется таблица:
| Xi | x1 | x2 | x3 | x4 | x5 |
| Pi | p1 | p2 | p3 | p4 | p5 |
 |
Для нее график – ломаная линия:
 |
Практически важной ситуацией является случай, когда необходимо определить вероятность попадания случайной величины в интервал значений. В этом случае вероятность будет равна разности функций распределения на концах этого интервала.
График функции F(x) непрерывных случайных величин:
Вероятность попадания вероятности СВ в заданный интервал от α до β:
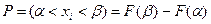 |
Функция распределения справедлива как для дискретных, так и для непрерывных СВ.
Плотность распределения вероятностей значений СВ представляет собой производную от функции распределения:  .
.
Пусть имеется некоторая СВ X, которая принимает значения x1, x2,…, xn и имеет функцию распределения F(X). Вероятность попадания вероятности СВ в интервал Δx:  . Разделим это выражение на Δx:
. Разделим это выражение на Δx:

– вероятность, приходящаяся на единицу этого интервала
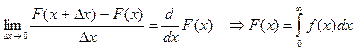 |
Плотность вероятностей – это отношение разности функций распределения на границах интервала к величине этого интервала, т.е. вероятность, приходящаяся на каждую единицу интервала.
 – вероятность попадания СВ в интервал (α,β).
– вероятность попадания СВ в интервал (α,β).
График плотности распределения вероятностей:
 |
Биномиальный закон распределения вероятностей:
p – вероятность появления события;
q = 1–p – вероятность появления обратного события.
Условие применимости биномиального закона распределения – он позволяет определить вероятность появления одного или двух событий.
Распределение Пуассона:  , где a – параметр распределения, который представляет собой среднюю вероятность появления события за время испытания.
, где a – параметр распределения, который представляет собой среднюю вероятность появления события за время испытания.
Экспоненциальное распределение: 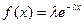 , где λ – параметр, учитывающий специфику изделий данного типа; f(x) – плотность вероятностей появления СВ x.
, где λ – параметр, учитывающий специфику изделий данного типа; f(x) – плотность вероятностей появления СВ x.
Для экспоненциального распределения λ = const, которая для каждого типа аппаратуры определяется путем статистических испытаний.
Свойство этого распределения – оно не зависит от начала отсчета времени.
 |
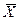 – нормированное значение в относительных единицах, т.е. интервал, в течение которого вероятность события уменьшается в e раз.
– нормированное значение в относительных единицах, т.е. интервал, в течение которого вероятность события уменьшается в e раз.
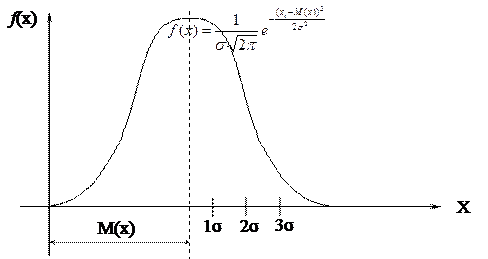 |
Закон распределения Гаусса:
σ – среднеквадратическое отклонение;
M(x) – математическое ожидание.
Область применения – потоки отказов постепенного характера, статистический контроль качества.
Показатели надежности АСОИиУ
Теория надежности позволяет определить качественные оценки, называемые показателями надежности. С их помощью можно объективно оценить надежность элементов, узлов, устройств, системы. Методы теории надежности являются вероятностными, поэтому они могут дать практические результаты, только если опираются на достаточный по объему статистический материал. Данные должны содержать информацию об отказах аппаратуры и ПО, а также о восстановлении работоспособности. Для ее получения ведутся наблюдения в течение длительного времени с документированием отказов и ремонтов.
Определение количества наблюдаемых объектов и длительности испытаний делается при помощи методов математической статистики, но общее правило гласит: чем больше статистики, тем достовернее результат.
Документальной формой сбора и накопления данных являются журналы статистического наблюдения, в которых фиксируются даты и причины отказов, время поиска и определения причин, время восстановления.
Фундаментальным понятием теории надежности, который определяет остальные понятия, является отказ. Под отказом понимают случайное событие, в результате которого объект теряет работоспособность и переходит в неработоспособное состояние. Потерей работоспособности является утрачивание хотя бы одной выполняемой функции или уход за допустимые пределы хотя бы одного эксплуатационного показателя. Допустимые пределы указываются в документации на изделие. Примеры отказов: повреждение микросхемы, потеря дорожки на носителе и т.д. Для устранения отказов и восстановления работоспособности требуются действия для нахождения места отказа, определения его причины и устранения.
Различают внезапные (мгновенные) и постепенные (износовые) отказы. Внезапный отказ происходит в результате скачкообразного, практически мгновенного изменения какого-либо параметра. Примеры: пробой электронно-дырочного перехода полупроводникового прибора, повреждение микросхемы разрядом статического электричества. Постепенные отказы вызываются медленным накоплением изменений в течение длительного времени (деградация). Примеры: износ головок записи/считывания, высыхание ленты в принтере, потеря эмиссии в электронно-лучевой трубке экрана.
Разновидностью отказов являются сбои. Сбоем называют самовосстанавливающийся отказ, который вызывает кратковременное нарушение работы. После сбоя система продолжает нормально функционировать. Сбой – это очень неприятное и коварное явление, из-за кратковременности и нерегулярности трудно его локализовать и устранить причину. В то же время, неприятностей при сбое может быть не меньше, чем при отказе, например, порча данных или микросхемы.
Основными показателями надежности являются интенсивностьотказов, вероятностьбезотказнойработы, вероятностьотказов, средняянаработканаотказ, среднеевремявосстановления.
 |
Интенсивность отказов λ – это один из наиболее важных в теоретическом и практическом отношениях показателей, который определяет законы распределения вероятностей отказов. В результате многочисленных исследований и обработки статистических испытаний установлено, что распределение вероятностей отказов подчиняется экспоненциальному закону надежности, параметром которого является λ. Таким образом, интенсивность отказов характеризует частоту появления отказов. В практических целях пользуются статистической оценкой появления отказов:
n – количество отказов, зафиксированное за время испытания Δt; N0 – количество испытуемых образцов.
Примечание. Имеется в виду испытание с восстановлением, при котором каждое отказавшее изделие восстанавливается и продолжает испытываться. Следовательно, N0 остается неизменным в течение всего срока испытания.
Если назвать 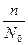 относительным количеством отказов за время Δt, то можно определить интенсивность отказов как относительное количество отказов, приходящееся на каждую единицу времени.
относительным количеством отказов за время Δt, то можно определить интенсивность отказов как относительное количество отказов, приходящееся на каждую единицу времени.
Примечание. Если образец один, то  , что дает более наглядное представление о физической природе интенсивности отказов.
, что дает более наглядное представление о физической природе интенсивности отказов.
Пример. Десять компьютеров испытывались 500 часов, зафиксировано 2 отказа. Интенсивность отказов:  .
.
Вероятность отказа Q(T0) – это вероятность появления отказа до конца заданного интервала T0, т.е. это вероятность того, что наработка до первого отказа окажется меньше T0. Таким образом, понятие вероятности отказа соответствует функции распределения при экспоненциальном
 |
законе с параметром λ, равным интенсивности отказов:
 |
Следовательно, плотность распределения вероятностей будет равна:
В данном случае случайной величиной будет время T, а ее реализацией – наработки T1, T2 и т.д.
Примечание. Вероятность отказа Q(T0) можно вывести из распределения Пуассона, если принять число событий, равным нулю.
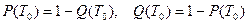 |
Вероятность безотказной работы P(T0) – это вероятность того, что объект сохранит работоспособность, т.е. не будет отказов в течение заданного интервала времени T0. При этом не имеет значения, сколько проработал объект к началу интервала. Вероятность безотказной работы и вероятность отказа образуют полную группу несовместных и противоположных событий, поэтому:
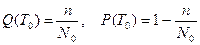 |
Их статистические оценки:
 |
n – количество отказов за время испытаний, N0 – количество испытуемых объектов.
Пример. В течение 600 часов испытывались 1000 микросхем. Зафиксировано 2 отказа. Вероятность безотказной работы: 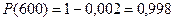 . Вероятность отказа:
. Вероятность отказа:  .
.
 |
Один из важнейших эксплуатационных параметров – это средняя наработка на отказ (MTBF – Mean Time Between Failures). MTBF – это математическое ожидание интервалов времени между соседними отказами. Средняя наработка на отказ может быть также в количествах циклов, количествах ударов.
 |
Статистической оценкой является Tср, где n – количество отказов за время испытаний, а ti – i-я наработка.
Пример. При испытании трех однотипных устройств было получено 5 отказов. Для первого устройства – 812 и 583, для второго – 821 и 1204, для третьего – 650. Общая наработка – 4070 ч. Средняя наработка на отказ – 817 ч.
Среднее время восстановления работоспособности объекта после отказа характеризует ремонтопригодность аппаратуры. Ремонтопригодность показывает степень приспособленности к проведению ремонтных работ и удобства их выполнения, а также выявляет трудоемкость и потребность в обслуживающем персонале. Среднее время восстановления по каждому виду аппаратуры позволяет рассчитывать численность и организацию ремонтной службы.
Случайное время восстановления tв складывается из трех переходов: tл – время, потраченное на локализацию отказа, tп – время определения причины отказа, tу – время устранения отказа. tв представляет собой математическое ожидание случайных времен восстановления. Его статистическая оценка: 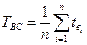 , где n – зафиксированное количество отказов за время испытания,
, где n – зафиксированное количество отказов за время испытания, 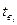 – случайное время восстановления после i-го отказа.
– случайное время восстановления после i-го отказа.
Потоки отказов
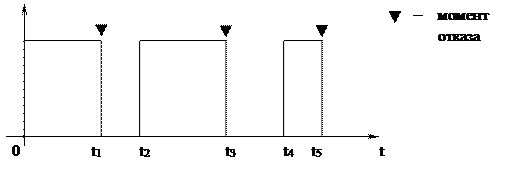 |
В процессе эксплуатации время от времени через случайные промежутки происходят отказы аппаратуры и ПО. После каждого отказа объект восстанавливается службой эксплуатации и продолжает функционировать до истечения срока службы в результате морального или физического износа.
0 – t1, t2 – t3, t4 – t5 – интервалы работы; t1 – t2, t3 – t4 – время восстановления; t1, t3, t5 – моменты отказов (периоды выключенного состояния и простоя здесь не показаны).
Имеют место потоки отказов с восстановлениями, которые характеризуются интенсивностью отказов, наработками и временами восстановления. Анализ системы с восстановлениями сложен и выходит за пределы данного курса, поэтому сделаем допущение, что потоки отказов и восстановлений разделены и существуют независимо друг от друга. Эти потоки подчиняются экспоненциальному закону, поэтому их можно отнести к пуассоновским потокам событий.
Потоком случайных событий (далее – поток) называют последовательность событий, происходящих друг за другом в случайные моменты времени, но подчиняющихся вероятностным закономерностям. Примеры: потоки отказов аппаратуры, поток заявок на обработку фотопленки и т.д. Пуассоновский поток – это такой поток, в котором число событий, приходящееся на любой интервал времени, подчиняется закону Пуассона.
Поток Пуассона имеет следующие свойства:
1) он является ординарным (обыкновенным), т.е. появление двух и более событий в один и тот же момент времени является практически невозможным;
2) поток стационарен, т.е. его вероятностные характеристики не изменяются во времени; в частности, на каждый временной интервал приходится постоянное среднее число событий;
3) вероятность появления очередного события в заданном интервале времени зависит только от длительности интервала, но не зависит от того, когда и сколько было событий до начала этого интервала. Пример: при неупорядоченном автобусном движении вероятность появления автобуса на остановке не зависит от времени его ожидания;
4) вероятность появления i событий в заданном интервале времени определяется законом Пуассона;
5) случайные интервалы времени между событиями подчиняются экспоненциальному закону.
 |
Поток Пуассона широко используется в теории надежности электронной аппаратуры. Это объясняется целым рядом причин: предоставляются очень удобные средства прогнозировать число отказов i (0, 1, 2, 3 и т.д.) в некотором заданном интервале времени.
Δt – интервал времени; λ – интенсивность отказов.
Определение параметра λ делается статистическим путем. Как частный случай, можно определить вероятность безотказной работы:  , и вероятность отказа:
, и вероятность отказа:  .
.
Интенсивность отказов λ является постоянной величиной, причем, чем сложнее аппаратура, тем больше это соответствует практике эксплуатации. Вероятность безотказной работы аппаратуры в течение заданного интервала времени p(t)не зависит от предшествующей работы аппаратуры, а зависит только от продолжительности интервала. Это значит, что будущее поведение объекта не зависит от прошлого, если в данный момент он исправен. К характерным свойствам потока отказов электронной аппаратуры можно отнести следующий: отказы представляют собой суммарное воздействие отказов элементов аппаратуры, которые независимы (отказы), многочисленны (элементы) и примерно одинаковы по степени влияния на надежность аппаратуры в целом.
Указанное свойство потока отказов позволяет построить его математическую модель. Многообразие подходов к построению математических моделей потоков отказов изначально определяет многообразие моделей. Далее рассматривается одна из них, называемая деградационной.
Математическая модель потока отказов представляет собой совокупность зависимостей, описывающих его поведение. Для удобства анализа их сводят к одному уравнению. Полученная вероятностная структура должна быть адекватной реальному физическому процессу функционирования объекта. Для создания математической модели можно воспользоваться различными исходными предпосылками. В данном случае рассматривается модель, основанная на физическом представлении о причинах отказов при экспоненциальном законе надежности.
Принятый подход относится и к внезапным, и к постепенным отказам, т.к. они, в принципе, имеют одну и ту же причину, в основе которой лежат различные деградационные процессы, приводящие к необратимому изменению параметров элементов. Разница только в том, что в первом случае определяющий параметр изменяется быстро и вызывает скачкообразное изменение состояния отказывающего элемента, а во втором случае определяющий параметр изменяется плавно и медленно. Под определяющими параметрами определяют физические параметры элементов, превышение допустимого значения которых выводит элементы из строя. Такими параметрами могут быть локальный перегрев, появление трещин и деформаций, механический износ, электрохимическая коррозия и многое другое. Как правило, определяющие параметры не поддаются контролю в процессе эксплуатации, т.к. существующие средства не способны на это. Универсальность – это главное достоинство деградационной модели потока отказов.
Деградационными называются физические, химические, механические процессы, способствующие отказам или вызывающие их. Причины и протекание этих процессов имеют случайный характер. Каждый элемент объекта имеет несколько параметров, характеризующих его свойства. Из большинства этих параметров любой может привести к отказу, если превысит допустимое значение. Один из них считается определяющим, остальные – вторичными, например, для микросхем определяющим с точки зрения теории надежности параметром является температура, а для дисковода – сила нажатия головки записи/чтения.
В электронной аппаратуре отказ одного элемента вызывает отказ всей системы. Система (объект) – это совокупность большого количества элементов, у которой определяющим является только один параметр. Отказ объекта наступает в результате отказа самого слабого элемента, когда его определяющий параметр превышает предельно допустимое значение.
Случайный процесс, при котором накопление деградационных изменений приводит к переходу системы из одного состояния, в данном случае – работоспособного, к другому (неработоспособному) при свойствах процесса, соответствующего пуассоновскому потоку событий, хорошо описывается при помощи цепей Маркова. Потоки отказов и восстановлений можно отнести к процессу Маркова, поскольку объект переходит из одного состояния к другому по мере того, как один из элементов отказывает, а потом восстанавливается и снова вводится в работу. При этом для системы неважно, как это делается – восстановлением элемента или его заменой. Отказы и восстановления элементов представляют собой этапы перехода системы от одного состояния к другому. Такое положение относится к стационарной цепи Маркова, а протекающий процесс можно описать с помощью уравнения Маркова.
 |
Задача определения времени до достижения предельного уровня описывается дифференциальным уравнением вида:
где x(t) – определяющий параметр деградационного процесса, A(t), B(t) – функции, характеризующие скорость изменения математического ожидания и дисперсии определяющего параметра, dh(t) – случайная составляющая, подчиняющаяся распределению Гаусса.
 |
Это уравнение представляет собой обобщенное описание изучаемого процесса, который является одним из процессов Маркова, а именно: процессом диффузионного типа. Чтобы использовать его применительно к электронной аппаратуре, необходимо считать его однородным. Это значит – протекающим с постоянной средней скоростью изменения параметров A(t), B(t), что вполне согласуется с практикой и не противоречит свойствам пуассоновского потока. Тогда после конкретизации функций A(t) и B(t) получаем исходное уравнение процесса:
где a – скорость изменения определяющего параметра x(t), b – коэффициент диффузии, который определяет скорость изменения дисперсии определяющего параметра.
 |
В этом уравнении коэффициенты a и b являются постоянными и уже не зависят от времени. Используя для описания диффузии уравнение Планка-Колмогорова, переходя от определяющего параметра к дифференциальному закону распределения вероятностей интервалов между отказами и решая полученное при этом дифференциальное уравнение, получаем в окончательном виде деградационную математическую модель потока отказов:
Конкретный вид модели зависит от того, из каких элементов состоит система и какими деградационными процессами задаются определяющие параметры этих элементов.
Если рассмотреть весь жизненный цикл объекта от схода с конвейера до списания по окончании срока службы, то обнаруживается, как показывает опыт эксплуатации, что поток отказов существенно меняется. Выделяются три резко неравных по длительности периода: начальный, основной и завершающий.
 |
Потоки отказов в этих периодах сильно отличаются по длительности и по характеру. Первый период t1 – это первоначальный ввод в эксплуатацию. Он сопровождается повышенной интенсивностью отказов внезапного характера. Их причиной являются скрытые дефекты комплектующих, попадание на сборку бракованных элементов, монтажные ошибки, плохие контакты и т.д. Эти отказы обнаруживаются в первые же часы или сутки работы (приработочные отказы). В условиях нормальной организации производства изготовитель проводит длительное испытание продукции в заводских условиях, поэтому у покупателя первый период может отсутствовать.
Интенсивность отказов быстро спадает и стабилизируется на более или менее постоянном уровне. Начинается основной период t2 (второй). Поток отказов становится пуассоновским. Основной период эксплуатации длится несколько лет. Упрощенно говоря – это срок службы аппаратуры, он может рассчитываться, исходя из показателей надежности элементов и узлов, или определяться экспериментально путем статистических испытаний. В основном периоде эксплуатации отказы могут быть как внезапными, так и постепенными. Они вызываются деградационными процессами всех видов, а также нарушением правил хранения и использования, ошибками пользователей, воздействием внешней среды и т.д. Математические методы теории надежности применимы именно к этому периоду.
В последнем периоде t3 возрастает и усиливается интенсивность потока отказов, которые приобретают преимущественно постоянный характер. Сказывается износ электромеханических элементов, старение полупроводниковых материалов, коррозия контактов, истечение срока службы деталей и т.д.
Блочная конструкция и открытая архитектура способствуют продлению срока службы, т.к. узлы и целые устройства легко заменяются. В зависимости от квалификации службы эксплуатации и наличия запасных деталей завершающий период может продлить срок службы на несколько месяцев и даже несколько лет.
Дата добавления: 2015-01-24; просмотров: 808;
