ПРЕДМЕТ І ЗАВДАННЯ ІСТОРІЇ ПЕДАГОГІКИ 1 страница. Кафедра «Вычислительная техника и информационные технологии»
Кафедра «Вычислительная техника и информационные технологии»
Курс лекций по предмету «Надежность и эксплуатация автоматизированных систем обработки информации и управления» для студентов специальности 22.02 «Автоматизированные системы обработки информации и управления» всех форм обучения.
СОДЕРЖАНИЕ
Введение....................................................................................................................................................... 2
Раздел I. Основы теории надежности....................................................................................................... 3
Основные понятия теории вероятностей.............................................................................................. 3
Основные теоремы теории вероятностей.............................................................................................. 5
Числовые характеристики случайных величин................................................................................... 6
Законы распределения случайных величин.......................................................................................... 8
Показатели надежности АСОИиУ....................................................................................................... 11
Потоки отказов....................................................................................................................................... 14
Раздел II. Эксплуатация аппаратных средств........................................................................................ 17
Общие сведения..................................................................................................................................... 17
Техническая документация................................................................................................................... 19
Рабочее место и условия эксплуатации............................................................................................... 19
Системный блок..................................................................................................................................... 20
Системная плата..................................................................................................................................... 20
Платы расширения................................................................................................................................. 22
Раздел III. Надежность и эксплуатация программного обеспечения.................................................. 24
Общие положения.................................................................................................................................. 24
Эксплуатация и защита ОС................................................................................................................... 26
Эксплуатация и защита файлов............................................................................................................ 27
Вирусы.................................................................................................................................................... 28
Архивирование данных........................................................................................................................ 29
Дефрагментация, оптимизация и коррекция дисков......................................................................... 31
Раздел IV. Модернизация аппаратных и программных средств.......................................................... 32
Основные принципы и технико-экономическое обоснование........................................................ 32
Модернизация системного блока......................................................................................................... 34
Модернизация дисковой памяти.......................................................................................................... 35
Модернизация видеоподсистемы......................................................................................................... 36
Модернизация подсистемы печати...................................................................................................... 37
Модернизация программного обеспечения........................................................................................ 37
Литература................................................................................................................................................. 38
Основная:................................................................................................................................................ 38
Дополнительная:.................................................................................................................................... 38
ВВЕДЕНИЕ
Предмет курса: изучение закономерностей появления и устранения неисправностей аппаратной части и программного обеспечения, изучение способов обеспечения работоспособности АСОИиУ в процессе эксплуатации.
Основу АСОИиУ составляют компьютеры (ПК). Компьютер представляет собой техническое изделие, которое характеризуется сложностью эксплуатационного обслуживания. Здесь и далее рассматривается не функциональное назначение, т.е. не использование для решения прикладных задач, а поддержание компьютеров в работоспособном состоянии. Под работоспособным понимается такое состояние, при котором объект способен выполнять все назначенные ему функции с сохранением характеристик и параметров в пределах, указанных в технической документации. Если не выполняется хотя бы одна из его функций или хотя бы один параметр не соответствует требованию, объект считается неработоспособным.
Сложность технического обслуживания компьютерного парка вызвано сложностью структуры и схемотехники ЭВМ, логических связей между компьютерами, процессов функционирования, разнообразием и большим количеством элементов, высокой плотностью монтажа, взаимодействием аппаратных и программных средств, большим объемом технической документации, необходимостью понимать тексты, сообщения на иностранном языке. Все это накладывает высокие требования к квалификации обслуживающего персонала (не пользователей!).
АСОИиУ как объект обслуживания имеет ряд особенностей, которые необходимо учитывать в процессе эксплуатации. ПК, а тем более компьютерная сеть,– это сложная, высокоорганизованная, автоматически действующая компьютерная система. Она состоит из многих разнородных, взаимосвязанных электронных и электромеханических компонентов с различными физическими принципами действия. Устройства ПК и их составные части связаны друг с другом электрическими, логическими и функциональными связями.
Функционирование ЭВМ представляет собой большое количество процессов, протекающих одновременно с большой скоростью и недоступных для непосредственного наблюдения.
ПК представляет собой нераздельную совокупность аппаратных и программных средств. При этом наиболее важная часть программного обеспечения – операционная система – это наиболее интеллектуальное достижение из всего, что когда-либо было создано человеком. Обслуживающий персонал должен одинаково хорошо знать «hardware» и «software».
В отличие от других систем, осуществляющих преобразование материальных объектов (видов энергии, формы и состояния материала), в ЭВМ происходит преобразование информации, что определяет и соответствующий интеллектуальный уровень систем этого класса.
ПК – это человеко-машинная система, в которой человек определенным образом общается и взаимодействует с машиной. ЭВМ является естественным продолжением и усилением мозга человека.
Одним из основных требований для эксплуатации ЭВМ является обеспечение надежности работы. Под надежностью изделия понимается свойство сохранять работоспособность и эксплуатационные показатели в течение требуемого времени, указанного в технической документации. ПК и компьютерное оборудование (сети, телеобработка, средства мультимедиа и т.д.) работают под воздействием случайных факторов. Случайными являются моменты обращения к ЭВМ, запрос той или иной программы, а также моменты нарушения работы и появления неисправностей. Поэтому для анализа работоспособности систем пользуются вероятностными методами.
Общие закономерности нарушения работоспособности различных объектов, их поддержание в исправном состоянии изучает теория надежности. Ее базой являются: математические методы теории вероятностей, теория массового обслуживания и математической статистики. Теориявероятностей предоставляет описание случайных событий и их свойств, числовые оценки случайных величин, законы распределения вероятностей появления случайных величин. Теориямассовогообслуживания позволяет изучить закономерности появления и устранения неисправностей, организовать систему обслуживания и ремонта. Методы математической статистики дают возможность планировать и проводить испытание объектов, определять их эксплуатационные параметры.
Основанная на этих методах теория надежности позволяет решить целый ряд больших и важных проблем, связанных с эксплуатацией аппаратных и программных средств АСОИиУ, в том числе:
· делать математическое описание закономерности появления неисправностей и создавать математические модели потока отказов и восстановлений;
· рассчитывать показатели надежности объектов;
· делать анализ надежности систем и их компонентов, выявлять ненадежные места и давать рекомендации по повышению надежности;
· сравнивать различные марки однотипного оборудования и делать обоснованный выбор;
· определять сроки службы изделий, проводить статистические испытания для экспериментального определения показателей надежности, элементов и устройств ЭВМ и компьютерного оборудования;
· рассчитывать потребность в запасных частях и расходных материалах;
· определять численность обслуживающего персонала.
РАЗДЕЛ I. Основы теории надежности
Основные понятия теории вероятностей
Основными показателями технической эффективности любой системы являются производительность и надежность. Проблема надежности включает вопросы поддержания физического (технического) состояния аппаратных и программных средств и обеспечения их работоспособности. Моменты появления отказов и сбоев, время поиска и устранения неисправностей, моменты появления ошибок в программах и продолжительность их поиска зависят от очень многих факторов и поэтому непредсказуемы, т.е. случайны. Неисправность может случиться через год, а может – через час. Поэтому невозможно предсказать точное время таких событий, а можно только прогнозировать их с большей или меньшей вероятностью.
Для определения этой вероятности необходимо знать законы распределения вероятностей случайных величин, например, отказов.
Теория вероятностей позволяет прогнозировать не всякие случайные события, а только такие из них, которые подчиняются статистическим законам распределения вероятностей. Эти законы устанавливаются путем статистических испытаний – путем организации опытов и наблюдения за ними с фиксированием результатов. Эти результаты подвергаются затем математической обработке.
Например, на испытание в течение определенного времени ставится партия принтеров, и фиксируются моменты отказов. Это дает возможность определить среднее время от отказа до отказа (MTBF). Пусть в лотерее участвует 100 человек. Разыгрывается 100 билетов, из которых 10 выигрышных. Выпадение выигрыша на одного из участников – дело случая (может выпасть, а может – нет), но эта ситуация подпадает под теорию вероятностей, т.к. имеется статистическая закономерность выпадения выигрыша, равная 0,1.
Несмотря на случайный характер нарушения работы АСОИиУ, пользователи и обслуживающий персонал имеют возможность прогнозировать поведение ПК в процессе эксплуатации и организовывать их ремонт и снабжение запасными деталями. Возможно также создать математическую модель процесса эксплуатации ЭВМ и даже сети, как сложной системы, функционирующей в среде воздействия случайных факторов. Математическая модель процесса эксплуатации задается совокупностью законов распределения ряда случайных величин, которые перед этим должны быть определены в результате статистических испытаний. К этим величинам относятся, например, средняя наработка на отказ, вероятность безотказной работы, среднее время восстановления и др.
Теория вероятностей, как раздел математики, появилась в связи с изучением азартных игр, но потом получила распространение во многих областях, особенно связанных с обслуживанием. Например, зная среднедушевое потребление хлеба в населенном пункте, можно правильно организовать работу пекарни. Пусть известно, что для поражения цели нужно 2,5 заряда. Ценна ли такая информация? На первый взгляд – бесполезная и весьма абсурдная. На самом деле эта величина позволяет обеспечить снабжение для поражения, например, 100 целей (250 снарядов). Еще точнее будет результат, если целей будет не 100, а 1000. В этом случае риск, что не будет хватать зарядов или останутся лишние, будет минимальным. При дальнейшем увеличении числа целей этот риск практически сводится к нулю. На интуитивном уровне делаем важный вывод: чем больше объем статистики, тем достовернее результат.
Одним из основных понятий теории вероятностей является понятие событие. Под событием понимают любой факт, любое изменение состояния, которое может произойти, а может и не произойти в результате опыта, называемого испытанием. Классический пример опыта – подбрасывание монеты; событие – выпадание «орла». Событием может быть выход с конвейера неисправного телевизора. Событие принято обозначать буквами A,B,C,… События можно классифицировать по нескольким критериям.
Различают совместные и несовместные события. Совместными называют такие события, когда наступление одного из них сопровождается другим в одном и том же опыте. В противном случае событие является несовместным. Допустим, в урне лежат белые и черные шары. Если доставать их по два, не глядя, то могут быть извлечены белый и черный шары. Это – совместное событие. Если доставать по одному, то может быть или белый, или черный шар, а одновременное их появление невозможно.
Событие может быть достоверным, случайным или невозможным. Достоверное событие происходит всегда и при любых условиях. Случайное событие может произойти, а может и не произойти. Невозможное событие не может произойти ни при каких условиях. Различают еще практически достоверное событие и практически невозможное событие, которые не могут произойти, но почему-то происходят. Случайные события могут иметь равные шансы на появление. Такие события называют равновероятными.
Очень важным понятием является полная группа событий. Несколько событий образуют полную группу, если в результате опыта появляется хотя бы одно из них. Частным случаем является противоположное событие  (читается «не A»). Противоположное событие
(читается «не A»). Противоположное событие  появляется обязательно, если не произошло событие A, например, появление отказа принтера в течение 3-х месяцев работы является событием, противоположным отсутствию отказа за этот же период. Противоположные события A и
появляется обязательно, если не произошло событие A, например, появление отказа принтера в течение 3-х месяцев работы является событием, противоположным отсутствию отказа за этот же период. Противоположные события A и  несовместны и образуют полную группу событий.
несовместны и образуют полную группу событий.
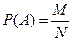 |
Количественной оценкой (численной мерой, численной характеристикой) возможности появления события является вероятность события. Классическое определение вероятности события по Лагранжу гласит: вероятность появления события A в опыте равна отношению числа случаев M, благоприятствующих событию, к общему числу случаев N:
Случай называется благоприятствующим событию, если влечет за собой появление этого события.
Вероятность события A может принимать значения от нуля до единицы в зависимости от того, какую долю составляет число случаев, благоприятствующих событию, от общего их числа, например, вероятность вытащить из колоды карт туза составляет  .
.
Классическое определение вероятности событий по Лагранжу дает теоретическую оценку, для получения которой требуется провести бесконечно большое число опытов. На практике пользуются приближенной оценкой, которая называется статистической вероятностью событий. Классическая и статистическая вероятности сходятся при неограниченном числе испытаний, например, классическая вероятность выпадания «орла» при подбрасывании монеты равна 0,5. При 4-х тысячах опытов отклонение от классической вероятности равно 0, 0069, а при 24-х тысячах опытов – 0,0005. Это положение носит название закона Бернулли (закон больших чисел).
Следствия из закона Лапласа:
1) вероятность невозможного события равна нулю, достоверного – единице;
2) вероятность появления какого-либо события из составляющих полную группу равна единице;
3)
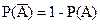 |
вероятность появления противоположных событий:
Пример 1. В коробке лежат 20 микросхем типа A и 30 микросхем типа B. Какова вероятность извлечения микросхем типа A?
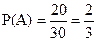 |
Число благоприятствующих случаев – 20, число всех событий – 30+20 = 50. Вероятность
Пример 2. В ящике находятся 10 бракованных и 15 хороших изделий. Если наугад выбрать 3 изделия, какова будет вероятность, что все изделия будут годными?
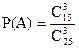 |
Число благоприятствующих случаев равно числу сочетаний из 15-ти по 3 –
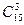 . Общее число случаев равно
. Общее число случаев равно 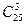 . Искомая вероятность:
. Искомая вероятность:
Пример 3. Вероятность отказа дисплея за 2 года работы равна 20%. Какова вероятность безотказной работы?
Имеется полная группа несовместных противоположных событий A и  , причем A = 20%. Следовательно, P(
, причем A = 20%. Следовательно, P(  ) = 1-P(A) = 80%.
) = 1-P(A) = 80%.
В заключение отметим, что в теории вероятностей понятие вероятности событий является фундаментальным.
Основные теоремы теории вероятностей
Совокупность нескольких событий образует сложное событие. К сложным событиям относятся сумма событий и произведение событий. Суммой событий A,B,C,… называется сложное событие, которое состоит в появлении события A, или события B, или события C и т.д.
Примечание. Здесь и далее рассматриваются только несовместные события, которые образуют полную группу. Можно сказать, что суммой несовместных событий, составляющих полную группу, является любое из этих событий.
Теорема 1. Вероятность появления любого из событий A,B,C,… равна сумме вероятностей этих событий: 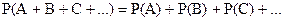 .
.
Пример 1. В коробке находится 30 транзисторов, 20 диодов и 50 резисторов. Какова вероятность, что из 2-х взятых наугад деталей одна окажется транзистором, а другая – диодом?
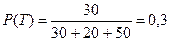 |
Вероятность выборки транзистора:
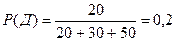 |
Вероятность выборки диода:
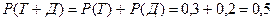 |
Искомая вероятность:
Пример 2. В лотерее разыгрывается 1000 билетов. На один из них падает выигрыш 500 руб., на 10 билетов – по 100 руб., на 50 билетов – по 20 руб., на 100 билетов – по 5 руб. Остальные билеты не выиграют. Какова вероятность, что купленный билет выиграет не менее 20 руб.?
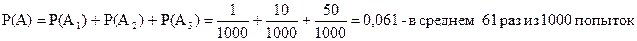 |
Обозначим A1 – выигрыш 500 руб., A2 – выигрыш 100 руб., A3 – 20 руб. A – выигрыш не менее 20 руб.
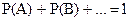 |
Следствие 1. Сумма несовместных событий, образующих полную группу, равна единице:
 |
Следствие 2. Сумма вероятностей двух противоположных событий равна единице:
Произведением двух и более событий называется одновременное появление всех этих событий.
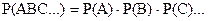 |
Теорема 2. Вероятность одновременного появления событий A,B,C,… равна произведению вероятностей этих событий:
Пример. Из партии ПК 80% имеют процессор Pentium, 90% имеют жесткий диск 1 Гб, 60% имеют тактовую частоту 150 Гц. Какова вероятность выбора наугад именно такого ПК?
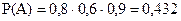 |
Вероятность выбора ПК с процессором Pentium P(A1) равна 0,8, с частотой 150 Гц P(A2) = 0,6, с диском 1 Гб P(A3) = 0,9. Искомая вероятность:
 |
Графическое толкование суммы и произведения событий:
Числовые характеристики случайных величин
Случайной называют величину, которая при опыте (испытании) принимает неизвестное заранее значение, которое меняется при повторном испытании в зависимости от непредсказуемых обстоятельств.
Различают дискретные и непрерывные случайные величины (СВ). Дискретные СВ принимают в результате опыта конечное число значений, например: количество дефектных деталей в партии, число факсов за сутки, количество отказов принтера в течение года, количество ошибок в программе. Непрерывные СВ могут принимать непредсказуемые значения из некоторого интервала, например: отклонение размера детали от эталона, время поиска неисправностей ПК, температура микросхемы во время работы.
Все множество значение, которое может получить случайная величина при испытании, называется генеральной совокупностью. Часть генеральной совокупности, принятая для рассмотрения, называется выборкой. Генеральная совокупность описывается числовыми характеристиками и законом распределения вероятностей СВ.
Для практических целей представляют интерес числовые характеристики дискретных СВ. Из них основными являются математическое ожидание и дисперсия.
Математическим ожиданием случайной величины называют вероятностную оценку ее среднего значения. Пусть имеется некоторая генеральная совокупность x1, x2,…, xn значений случайной величины X, полученных с вероятностями p1, p2,…, pn. В общем виде математическое ожидание M(X) случайной величины X представляет собой среднее значение, взвешенное по
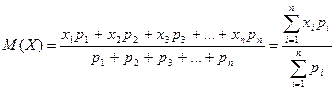 |
вероятностям, т.е. средневзвешенное значение:
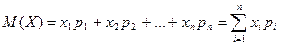 |
Генеральная совокупность представляет собой полную группу несовместных событий, поэтому
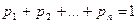 . Следовательно:
. Следовательно:
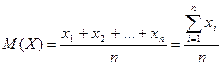 |
Для частного, но очень важного для практики случая равновероятных исходов (p1 = p2 =…) математическое ожидание вырождается в среднее арифметическое:
Свойства математического ожидания:
1)
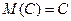 |
математическое ожидание постоянной величины есть сама постоянная величина:
 |
2) постоянный множитель случайной величины X можно выносить за знак математического ожидания:
3) математическое ожидание суммы двух генеральных совокупностей есть сумма их математических ожиданий:
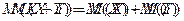 |
4) математическое ожидание произведения двух генеральных совокупностей есть произведение их ожиданий:
Пример. В некотором регионе имеется один город с населением 500 тыс. человек, пять городов с населением 200 тыс. человек и четырнадцать городов по 50 тыс. жителей. Какова средняя численность одного города в этом регионе?
Вероятность выбора города с населением 500 тыс. человек: 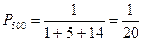
Аналогично:  и
и 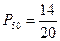
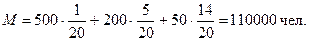 |
Средняя численность представляет собой математическое ожидание:

Примечание. Если вычислить результат как среднее арифметическое, то будет недопустимая ошибка: 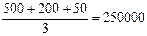 .
.
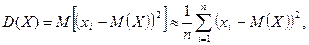 |
Каждое значение xi отличается от ее математического ожидания M(X), т.е. имеет отклонение от среднего. Характеристикой рассеяния случайной величины от ее математического ожидания служит дисперсия случайной величины:
x1, x2,…, xi,…, xn – генеральная совокупность
n – число членов генеральной совокупности
M(X) – математическое ожидание случайной величины
xi-M(X)2 – отклонение СВ от математического ожидания
В теоретических исследованиях рассеяние случайной величины оценивают дисперсией; на практике больше подходит среднеквадратичное отклонение:  В некоторых случаях используется характеристика, называемая модой Mo. Мода Mo(X) случайной величины X – это наиболее вероятное ее значение.
В некоторых случаях используется характеристика, называемая модой Mo. Мода Mo(X) случайной величины X – это наиболее вероятное ее значение.
Дата добавления: 2015-01-24; просмотров: 752;
