Уравнение Бернулли для потока реальной жидкости

Полученные выводы уравнения Бернулли для элементарной струйки можно распространить на слабо деформированный установившийся поток. При этом предполагается, что поток представляет собой совокупность элементарных струек и вблизи любого рассматриваемого сечения имеет место плавное и медленное изменение движения. Кроме того, следует иметь в виду, что в плоскости живого сечения слабо деформированного потока, как и для элементарной струйки, давление распределяется по гидростатическому закону. При таком допущении уравнение Бернулли для целого потока реальной жидкости можно получить суммированием полных удельных энергий элементарных струек, с учетом происходящих потерь энергии по длине потока.

Если полная удельная энергия элементарной струйки 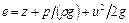, а элементарный весовой расход 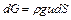, то энергия элементарного весового расхода струйки будет равна:

.

Интеграл уравнения будет равен энергии весового расхода целого потока жидкости Е, т. е.

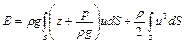
Энергия потока жидкости характеризуется, таким образом, двумя интегралами. Величина первого интеграла определяет значение потенциальной, а второго – кинетической энергии весового секундного расхода жидкости.

Так как в плоскости живого сечения 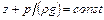, то первый интеграл можно представить в таком виде:

.

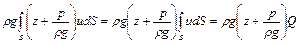Рассмотрим второй интеграл. Как уже отмечалось, движение потока характеризуется средней скоростью u_ср в данном сечении, отклоняющейся от местной скорости u в точке на положительную или отрицательную величину Du. Следовательно,

.

Подставив это выражение под знак второго интеграла, получим

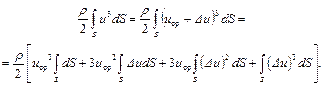
Второй интеграл в последней формуле равен нулю. Действительно,

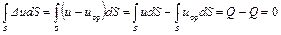
Четвертый интеграл 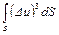также может быть принят равным нулю, так как отклонения Du могут быть положительными и отрицательными, а по величине весьма незначительны по сравнению с величиной средней скорости u_ср. При суммировании как положительных, так и отрицательных отклонений Du³ в результате получится величина интеграла, приближающаяся к нулю. Следовательно,

.

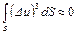С учетом полученных выражений

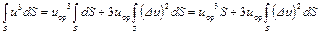
или

.

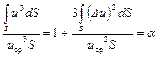Следовательно,

,

где a учитывает неравномерность распределения скоростей по живому сечению потока и называется коэффициентом кинетической энергии. Коэффициент a выражает отношение интегральной, т. е. действительной кинетической энергии весового секундного расхода потока к его средней кинетической энергии, вычисленной по средней скорости в данном сечении.

Величина коэффициента a обычно определяется опытным путем. Для установившегося слабо деформированного потока по данным опытов 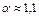. Для развившегося ламинарного движения 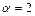. Однако при большой неравномерности распределения скоростей коэффициент может принимать большие значения.

Подставляя в уравнение, определяющее энергию весового расхода всего потока жидкости, найденные значения интегралов, получим:

.

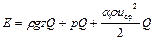Разделив это уравнение на весовой расход потока , получим удельную энергию жидкости Е, протекающей в единицу времени через рассматриваемое живое сечение потока:

.

Полученная зависимость применима к любому сечению потока. Если, например, u_ср1 и u_ср2 – средние скорости в двух разных сечениях, p₁ и р₂ – гидродинамические давления в центрах тяжести этих сечений, a a₁ и a₂ – соответствующие коэффициенты кинетической энергии, то применительно к двум избранным сечениям можно написать:

.

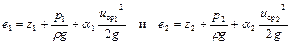Вследствие наличия гидравлических сопротивлений при движении реальной жидкости, часть энергии расходуется по длине потока на преодоление этих сопротивлений. Поэтому в последующем (во втором) сечении энергия потока будет меньше, чем в первом сечении, на величину h_w равную части энергии, необратимо превращенной в тепловую энергию. Следовательно,

.

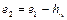Учитывая изложенное на основании сохранения энергии, получим для любых двух рассматриваемых сечений следующее выражение:

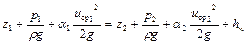. (1.33.)

Полученное уравнение является уравнением Бернулли для потока реальной жидкости.

Потеря полного напора на единицу длины потока также называется гидравлическим уклоном потока i, т.е.

.

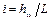В случае, когда поток движется по каналу (трубе) постоянного сечения, то на основании постоянства расхода при установившемся движении кинетическая энергия не изменяется, так как скорости везде постоянны. В таком случае

,

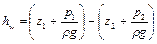где h_w – потеря потенциальной энергии потока на участке длиной L. Эта потеря потенциальной энергии (напора) на единице длины потока называется пьезометрическим уклоном потока i_p:

.

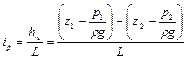Для потока в горизонтальной трубе постоянного сечения 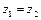. Тогда

.

Из уравнения следует, что уменьшение пьезометрической высоты равно высоте потерянного напора на данном участке потока.

Уравнение (1.33) широко используют для определения скоростей и расходов жидкостей; гидравлических расчетов напорных трубопроводов, насосных установок, гидравлических турбин, сепараторов; расчетов водоструйных насосов, карбюраторов и т.п.