Истечение жидкости через малое отверстие в тонкой стенке при постоянном напоре
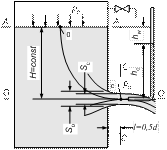 Для определения скорости установившегося истечения жидкости под постоянным напором через малое отверстие в тонкой стенке воспользуемся уравнением Бернулли для точек «0» и «с», находящихся на одной траектории
Для определения скорости установившегося истечения жидкости под постоянным напором через малое отверстие в тонкой стенке воспользуемся уравнением Бернулли для точек «0» и «с», находящихся на одной траектории
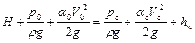 .
.
Последнее слагаемое в правой части уравнения представляет собой потерянную часть напора вследствие трения жидкости о стенки отверстия и ее деформации. Его значение определяют по формуле для потерь напора в местных сопротивлениях
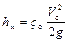 .
.
Вследствие потери напора при прохождении жидкости через отверстие напор hc в сечении струи С-С, измеренный при помощи трубки Пито, окажется меньше геометрического напора H. Он равен скоростному напору жидкости в рассматриваемом сечении
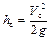 .
.
Отношение потерянного напора hw к напору, превращенному в скоростную энергию hc, представляет собой коэффициент сопротивления 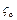 , учитывающий местные потери энергии в пределах отверстия.
, учитывающий местные потери энергии в пределах отверстия.
Представим приведенное выше уравнение Бернулли в следующем виде
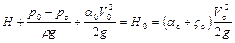 ,
,
где H0 – полный напор.
При постоянном напоре H в резервуаре скорость V0 на свободной поверхности жидкости равна нулю. Тогда из последнего уравнения найдем скорость в сжатом сечении струи
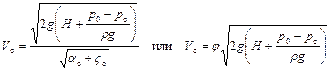 ,
,
где 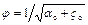 – коэффициент скорости.
– коэффициент скорости.
При истечении идеальной жидкости, для которой 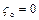 и
и 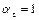 , скорость движения в струе максимальная, равная
, скорость движения в струе максимальная, равная
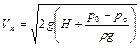 .
.
Таким образом, коэффициент скорости представляет собой отношение скоростей истечения реальной и идеальной жидкостей.
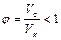 .
.
Он учитывает местные гидравлические сопротивления в отверстии и неравномерность распределения скоростей в сжатом сечении.
Сжатие струи, вытекающей из отверстия, учитывают при помощи коэффициента сжатия 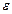 , который равен отношению площади струи Sс в узкой ее части к площади отверстия Sо
, который равен отношению площади струи Sс в узкой ее части к площади отверстия Sо
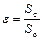 .
.
Объемный расход жидкости, протекающей через узкое сечение струи
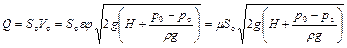 , (1.34)
, (1.34)
где 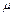 – коэффициент расхода.
– коэффициент расхода.
Так как теоретический расход определяют как
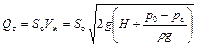 ,
,
то коэффициент расхода представляет собой отношение действительного расхода к теоретическому
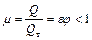 .
.
Дата добавления: 2015-01-24; просмотров: 1097;
