Уравнение Бернулли для несжимаемой жидкости и примеры его применения

При течении капельных жидкостей и газов, когда скорость движения последних значительно меньше скорости распространения в них звуковых колебаний [V<(100¸150) м/с], сжимаемостью среды можно пренебречь и считать ее плотность постоянной. В этом случае функция давления становится равной

.

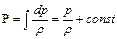Рассматривая в качестве массовых сил только силы тяжести, обладающие потенциалом 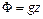, преобразуем интеграл Бернулли к виду

, (1.32)

который получил название уравнения Бернулли.

Для двух точек, расположенных на одной и той же линии тока в разных сечениях потока идеальной несжимаемой жидкости, это уравнение записывают в одной из следующих форм:

.

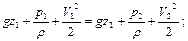
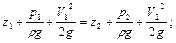
Уравнение Бернулли имеет также и энергетический смысл.

Геометрическая высота z, или геометрический напор, представляет собой удельную потенциальную энергию положения.

Пьезометрическая высота 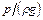, или пьезометрический напор, создаваемый давлением р жидкости плотностью r, представляет удельную потенциальную энергию давления.

Скоростная высота, или скоростной напор 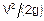представляет удельную кинетическую энергию.

Сумма этих трех величин, т. е. полный гидродинамический напор, выражает собой полную удельную энергию жидкости в поперечном сечении элементарной струйки, которая, согласно уравнению Бернулли, есть величина постоянная.

Таким образом, в установившемся движении полная удельная энергия частиц совершенной жидкости, составляющих элементарную струйку, сохраняется постоянной по всей длине струйки. Следовательно, уравнение Бернулли является специальным выражением общего основного физического закона сохранения энергии применительно к рассматриваемому движению жидкости.

Необходимо отметить, что здесь, а также и в дальнейшем, имеется в виду изотермическое движение жидкости, т. е. при неизменной ее температуре.