Уравнение движения идеальной жидкости и его решения

Уравнение движения идеальной жидкости получают путем исключения из уравнения Навье-Стокса (1.16) слагаемых, в которых в качестве сомножителя имеется коэффициент динамической вязкости

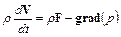. (1.22)

Полученное выражение называют уравнением Эйлера для идеальной жидкости.

Полная производная вектора скорости по времени математически эквивалентна сумме слагаемых, в которые входят удельная кинетическая энергия жидкой частицы ( ) и вектор угловой скорости

.

Подстановка этого выражения в уравнение (1.22) преобразует последнее в уравнение движения идеальной жидкости в форме Громеки-Ламба

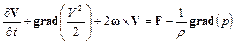. (1.23)

В гидравлике широко используют понятие потенциала, который выступает в качестве характеристики векторного поля /24/. Векторное поле называют потенциальным, если существует такая скалярная функция 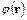– потенциал векторного поля, градиент которой в рассматриваемой точке равен вектору в этой же точке, т.е.

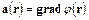. (1.24)

Для потенциального поля справедливо условие

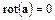. (1.25)

Объемные силы, под действием которых возможно равновесие жидкости, имеют потенциал. Например, сила тяжести имеет потенциал и выражается через него в соответствии с (1.24)

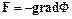. (1.26)

В уравнение движения входит плотность жидкости, зависящая в общем случае от температуры и давления. Однако в природе происходит множество процессов (изотермических , адиабатных , политропных ), в которых плотность однозначно определяется только давлением 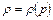. Жидкость, у которой плотность является функцией только давления, называют баротропной. Для нее непосредственно можно вычислить интеграл , который называют функцией давления

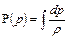. (1.27)

Поскольку

,

то путем следующих формальных преобразований получаем

.

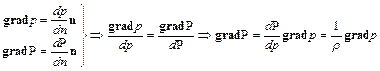Величина представляет собой главный вектор сил давлений в данной точке, отнесенный к единице массы, т.е. вектор объемного действия сил давления. Таким образом, функция давления 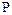, градиент которой равен вектору объемного действия сил давления, представляет потенциал объемного действия сил давления.

Заменив в уравнении движения идеальной жидкости в форме Громеки-Ламба (1.23) массовые силы и силы давления на выражения через их потенциалы, получим векторную форму уравнения Эйлера-Громеки:

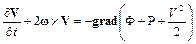. (1.28)

Рассмотрим некоторые решения этого уравнения.

Интеграл Эйлера является решением уравнения Эйлера-Громеки в случае потенциального установившегося движения.

Потенциальным называют движение жидкости, поле скоростей которой имеет потенциал , следовательно

.

Потенциальное течение всегда безвихревое, т.е. в нем отсутствует вращение жидкости, характеризуемое вектором угловой скорости

.

Установившимся называют движение, у которого скорость не изменяется с течением времени. Поэтому

.

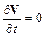Для потенциального установившегося течения уравнение Эйлера-Громеки примет вид

.

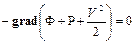Равенство нулю градиента функции означает, что

. (1.29)

Это выражение называют интегралом Эйлера.

В случае действия на жидкость только сил тяжести 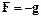, потенциал массовых сил определяется следующим выражением:

.

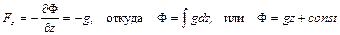Заменяя в интеграле Эйлера потенциал массовых сил и функцию давления их выражениями, получим уравнение Эйлера

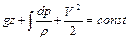, (1.30)

где – потенциальная энергия положения частицы жидкости единичной массы в поле сил тяжести; – потенциальная энергия объемного действия сил давления; – кинетическая энергия частицы жидкости единичной массы.

С точки зрения механики уравнение Эйлера представляет собой закон сохранения энергии для потенциального установившегося течения жидкости – сумма всех видов энергии, отнесенных к единице массы жидкости, во всех точках потока имеет одно и то же значение.

Интеграл Бернулли представляет собой решение уравнения Эйлера-Громеки в случае установившегося не потенциального движения.

При установившемся не потенциальном (вихревом) течении справедливы следующие выражения:

,

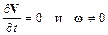т.е. не происходит изменения скорости жидкости во времени, а ее частицы имеют возможность участвовать во вращательном движении. Для таких потоков уравнение Эйлера-Громеки (1.28) примет вид

.

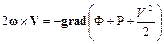В условиях установившегося движения линии тока и траектории совпадают. Элемент пути, пройденного частицей жидкости вдоль траектории в направлении течения, определяют по формуле

.

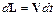Найдем скалярное произведение уравнения Эйлера-Громеки и полученного выражения

.

Левая часть данного уравнения равна нулю, так как является скалярным произведением двух взаимно-перпендикулярных векторов . Следствием этого является равенство нулю первого сомножителя, стоящего в правой части уравнения, поскольку элемент пути отличен от нуля.

.

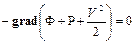Равенство нулю градиента функции в условиях установившегося потока означает, что

. (1.31)

Это выражение называют интегралом Бернулли. Из него следует, что в установившемся не потенциальном потоке сумма всех видов энергии постоянна лишь вдоль одной и той же траектории (линии тока).

Выделенная фраза подчеркивает отличие интеграла Бернулли от интеграла Эйлера, справедливого для любых точек установившегося потенциального потока.