Динамика идеальной жидкости

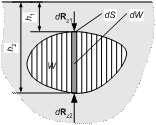Рассмотрим тело произвольной формы, полностью погруженное в жидкость. По всем направлениям на него действуют силы гидростатического давления.

Горизонтальные силы взаимно уравновешиваются, так как для любой точки на поверхности тела имеется с противоположной стороны на такой же глубине другая точка, находящаяся под действием такого же гидростатического давления.

Для определения вертикальной составляющей силы давления жидкости на тело разобьем его мысленно на элементарные вертикальные объемы dW цилиндрической формы, площади поперечного сечения которых обозначим dS. На верхнюю и нижнюю поверхности выделенного цилиндра действуют силы

,

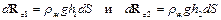направления которых взаимно противоположные. Их равнодействующая – элементарная подъемная сила

.

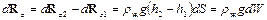Интегрируя полученное выражение по всему объему, считая плотность жидкости постоянной, получим выталкивающую силу, действующую на тело, погруженное в жидкость

.

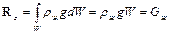Данное выражение является математической формулировкой закона Архимеда, согласно которому на погруженное в жидкость тело действует выталкивающая сила, равная весу вытесненной им жидкости.

Объем жидкости, вытесненной погруженным телом, называют объемным водоизмещением. Центр тяжести объемного водоизмещения получил название центра водоизмещения (центра величины). Точка приложения подъемной силы лежит в центре водоизмещения В.

Собственный вес твердого тела G_т приложен в центре тяжести тела С (если плотность тела неоднородна, то в общем случае геометрический центр тяжести и центр тяжести тела не совпадают).

В зависимости от соотношения величин подъемной силы и веса погруженного в жидкость тела возможны следующие состояния тела:

G_т > R_z – тело тонет;

G_т < R_z – тело всплывает;

G_т = R_z – тело плавает в погруженном (безразличном) состоянии.

Последнее равенство является одним из условий равновесия тела в жидкости. Другое условие равновесия заключается в равенстве нулю моментов всех сил, действующих на погруженное тело. Оно выполняется в том случае, когда центр тяжести тела С и центр водоизмещения В лежат на одной вертикальной оси.

Способность плавающего тела восстанавливать после крена исходное положение называют остойчивостью.

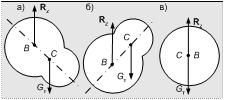Рассмотрим различные случаи взаимного расположения центров тяжести и водоизмещения.

Если центр тяжести С расположен ниже центра водоизмещения В, то положение тела устойчивое (рис.а). Будучи выведенным из положения равновесия внешней силой, оно стремится вернуться в прежнее равновесное состояние.

При расположении центра водоизмещения В ниже центра тяжести С положение становится неустойчивым, т.е. при отклонении от состояния равновесия по любой причине тело в исходное состояние не возвращается (рис. б).

При совпадении центров С и В однородное тело может находиться в равновесии при любом положении (рис. в).

Все эти выводы распространяются и на тела, частично погруженные и плавающие на поверхности жидкости. В таких случаях принимается во внимание не полный объем плавающего тела, а лишь та его часть, которая погружена и равна объему вытесненной жидкости.

На законе Архимеда основан технический способ определения плотности жидкости посредством ареометра – пустотелой цилиндрической трубки, нижняя часть которой утяжелена с помощью шарика или гильзы. Ареометр погружается в испытываемую жидкость и плавает в ней в вертикальном положении благодаря грузу, имеющемуся в шарике или гильзе. Глубина погружения, отсчитываемая по шкале, нанесенной на трубке, соответствует плотности жидкости.

Динамика идеальной жидкости

Идеальной называют воображаемую жидкость, лишенную вязкости и теплопроводности. В ней отсутствует внутреннее трение, она непрерывна и не имеет структуры. Такая идеализация для многих течений допустима, и дает хорошее соответствие при описании реальных течений жидкостей и газов на достаточном удалении от омываемых твердых поверхностей и поверхностей раздела с неподвижной средой.