Получение критериев подобия методом масштабных преобразований

Любое дифференциальное уравнение можно привести в безразмерную форму, заменяя исходные переменные на безразмерные путем соответствующих тождественных преобразований.

Под безразмерной переменной понимают исходную переменную, деленную на соответствующий масштаб. В качестве масштаба выбирается одноименная физическая величина, известная по условию задачи (т. е. входящая в условия однозначности). Этот прием называется методом масштабных преобразований. Рассмотрим его на примере системы уравнений для вынужденного движения несжимаемой жидкости. Для простоты рассматриваем стационарный процесс, т. е. .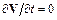

В качестве масштабов можно выбрать следующие известные величины: масштаб длины l – характерный линейный размер, например длина обтекаемого тела или диаметр трубы и т. п. Масштаб скорости w₀ – скорость набегающего потока или средняя скорость в канале и т. п. Масштаб давлений 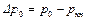– разность между давлением на входе и выходе из канала.

Масштаб давлений обычно выбирают в виде разностей, потому что давление входят в исходные уравнения только под знаком дифференциала. В этом случае для сокращения числа влияющих факторов удобно перейти от переменной р к (р₀–р), причем .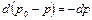

Введем следующие новые переменные:

безразмерные координаты: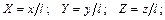

безразмерную скорость и ее составляющие: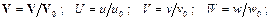

безразмерное давление .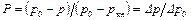

Можно доказать, что у подобных явлений в сходственных точках (а для нестационарных процессов и в сходственные моменты времени) безразмерные переменные равны.

Рассмотрим безразмерные координаты сходственных точек а и a': 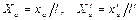, но по условию подобия 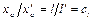. Применяя к последнему выражению правило перестановки членов пропорции, получаем 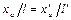, следовательно, 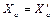. Аналогично 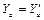и .

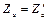У подобных явлений подобны поля скоростей, т. е. для любой составляющей скорости, например, по оси х можно записать 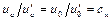. Перестановкой членов пропорции отсюда получаем 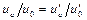, т. е. .

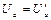Аналогичные выводы можно сделать для всех безразмерных переменных. Таким образом, у подобных явлений поля безразмерных величин тождественны.

Теперь введем новые переменные в дифференциальные уравнения процесса. Для того чтобы преобразования были тождественными, будем каждую переменную не только делить, но и умножать на соответствующий масштаб.

Уравнение движения для сокращения выкладок рассмотрим только в проекции на одну из координатных осей, например на ось x. Операция перевода к безразмерной форме приводит к следующему выражению:

.

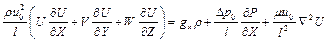Если разделить это выражение на множитель у последнего члена 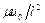, то получим дифференциальное уравнение движения в безразмерной форме

.

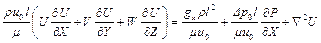Поскольку безразмерные переменные, входящие в это уравнение, равны для всех подобных явлений, то для подобных явлений должны быть одинаковыми и безразмерные комплексы размерных величин, входящие в него в виде множителей 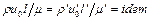; ; 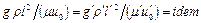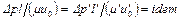, т.е. каждый из этих комплексов можно считать критерием гидродинамического подобия. Полученные здесь три безразмерных комплекса принято выражать через три общепринятых критерия Re, Fr и Eu:

;

;

.

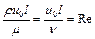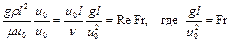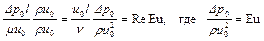Таким образом, уравнение движения в проекции на ось x в безразмерной форме имеет вид

.

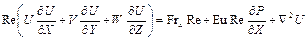Уравнение сплошности в безразмерной форме имеет вид

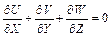
и новых критериев не дает.