Давление жидкости на криволинейную поверхность

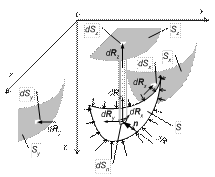Рассмотрим жесткую, невесомую, криволинейную поверхность площадью S, находящуюся внутри жидкости. На каждую элементарную площадку dS_n рассматриваемой поверхности действует сила 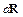, направленная по нормали к ней

.

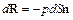Вся поверхность S нагружена системой таких непараллельных сил давления жидкости. В данном случае проще определить не вектор равнодействующей силы 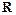, а его проекции R_x, R_y и R_z на оси координат. Эти проекции равны суммам проекций элементарных сил на соответствующие оси, так как последние образуют системы параллельных сил.

.

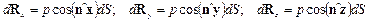Учитывая, что

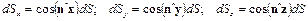
получим проекции элементарной силы давления, действующей на площадку dS

,

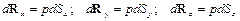или

.

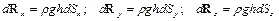Проекции результирующей силы давления, действующей на всю криволинейную поверхность, погруженную в жидкость, равны

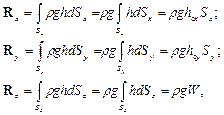
где h_cx и h_cy – вертикальные координаты центров тяжести проекций S_x и S_y криволинейной поверхности S на плоскости yoz и xoz, соответственно; W – объем жидкости, заключенный между S и свободной поверхностью жидкости, называемый в гидравлике объемом тела давления.

Проекции результирующей силы давления жидкости, действующей на криволинейную поверхность S, на горизонтальные оси равны силам давления, действующим на проекции S_x и S_y этой поверхности на вертикальные координатные плоскости, перпендикулярные соответствующим осям. Проекция результирующей силы на вертикальную ось равна весу жидкости, заключенной в объеме вертикального столба, опирающегося на заданную криволинейную поверхность, а сверху ограниченного плоскостью свободной поверхности.