Определение силы, действующей на наклонную пластину, погруженную в жидкость
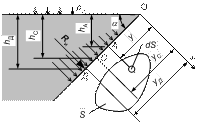 Рассмотрим плоскую стенку площадью S, смачиваемую жидкостью и наклоненную под углом a.
Рассмотрим плоскую стенку площадью S, смачиваемую жидкостью и наклоненную под углом a.
Давление жидкости, действующее на элемент ее поверхности площадью dS, расположенный на глубине h, составляет
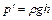 ,
,
следовательно, элементарная сила от этого избыточного давления будет равной
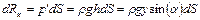 ,
,
где y – расстояние от оси Ox, расположенной на свободной поверхности жидкости, до рассматриваемой площадки вдоль пластины.
Результирующую силу найдем интегрированием элементарной силы по всей поверхности S.
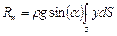 .
.
Интеграл в данном выражении представляет собой статический момент площади стенки относительно оси Ox. Он равен
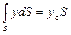 ,
,
где yс – расстояние от центра тяжести площади стенки до рассматриваемой оси.
Поэтому
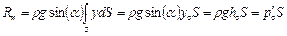 ,
,
где hс – глубина расположения центра тяжести пластины; 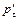 – давление жидкости в центре тяжести пластины.
– давление жидкости в центре тяжести пластины.
Таким образом, значение результирующей силы давления жидкости на наклонную плоскую поверхность представляет собой произведение давления жидкости, действующего в центре тяжести этой поверхности, на ее площадь.
В закрытом сосуде с избыточным давлением на свободной поверхности жидкости, равным p0, гидростатическое давление в центре тяжести равно
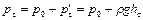
и результирующая сила давления на стенку рассчитывается по формуле
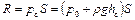 .
.
Для определения центра приложения результирующей силы – центра давления, запишем уравнение моментов относительно оси, проходящей через точку О, расположенную на поверхности жидкости.
Элементарный момент dМ, создаваемый элементарной силой dRи относительно оси Оx равен
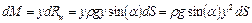 .
.
Интегрирование данного уравнения по всей поверхности пластины дает результирующий момент
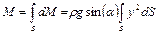 .
.
Выражение, стоящее под знаком интеграла, есть момент инерции площади фигуры Jx относительно оси Оx, т.е.
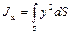
и подстановка его в предыдущее уравнение приводит к следующему результату
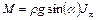 .
.
Этот момент так же может быть представлен в виде произведения результирующей силы на координату центра давления относительно выбранной оси, измеренную вдоль пластины
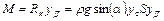 .
.
Приравняв последние два уравнения, получим
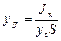 .
.
Момент инерции площади фигуры относительно оси Оx представляют в виде суммы
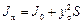 ,
,
где J0 – момент инерции площади пластины относительно оси, проходящей через центр тяжести этой площади и параллельной Оx.
Вследствие этого окончательно получим
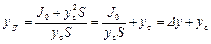 .
.
Дата добавления: 2015-01-24; просмотров: 1546;
