Основное уравнение гидростатики. Закон Паскаля

Равенство нулю вектора скорости частицы жидкости позволяет исключить из уравнения Навье-Стокса (1.16) все слагаемые, зависящие от него. Полученное в результате этого уравнение называют основным дифференциальным уравнением равновесия жидкости

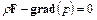. (1.18)

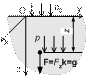Уравнение (1.18) можно представить в проекциях на оси координат. Располагая оси таким образом, что одна из них (ось z) совпадает с направлением действия главного вектора плотности объемных сил ( 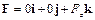), получим

.

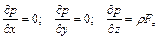Первые два уравнения указывают на независимость давления от координат x и y, т.е. поверхностями равного давления являются плоскости, перпендикулярные направлению действия главного вектора плотности объемных сил.

Интегрирование последнего уравнения, в случае действия только силы тяжести (F_z = g) и при условиях:

постоянства плотности ;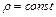

постоянства давления, действующего на свободную поверхность находящейся в покое жидкости ;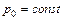

выбора начала координат на свободной поверхности жидкости

,

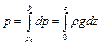дает основное уравнение гидростатики

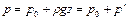, (1.19)

где – давление жидкости.

Из него следует, что давление в любой точке покоящейся жидкости равно внешнему давлению, сложенному с весом столба жидкости, имеющего площадь основания, равную единице и высоту, отсчитываемую от свободной поверхности жидкости по нормали к ней до рассматриваемой точки.

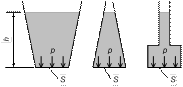Согласно этому уравнению, давления, оказываемые на донышки сосудов различной формы, заполненных жидкостью до одного и того же уровня h, одинаковы. При равенстве площадей донышек S это приведет к одинаковым силам, действующим на них со стороны жидкости. Данный феномен, позволяющий малым количеством жидкости создавать большие усилия, называют "гидростатическим парадоксом".

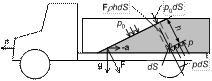Рассмотрим равновесие жидкости при наличии негравитационных массовых сил. Предположим, что бак установлен на автомобиле, движущемся с постоянным ускорением 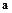. Массовая сила, действующая на жидкость, равна сумме силы тяжести и силы инерции переносного движения. Результирующая массовая сила, отнесенная к единице массы (плотность массовых сил) определяется по формуле

.

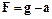Обозначим давление на свободной поверхности жидкости p₀, а давление на глубине h – p. Частицы жидкости, находящиеся на площадке dS, расположенной на глубине h,будут находиться в равновесии относительно стенок бака, если выполняется следующее уравнение

,

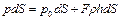из которого следует

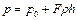. (1.20)

Уравнение (1.20) является основным уравнением гидростатики для относительного покоя при прямолинейном равноускоренном движении.

Если ускорение при прямолинейном равноускоренном движении равно ускорению свободного падения по величине и направлению ( 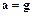), то массовые силы в жидкости становятся равными нулю ( 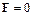) и давление внутри жидкости станет равным давлению на ее свободной поверхности, т.е. жидкость окажется невесомой.

Поверхностями уровня являются плоскости, перпендикулярные результирующей массовой силе .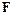

Отсутствие движения жидкости означает равенство нулю и скорости ее деформационного движения. Следствием этого, является равенство нулю тензора напряжений в жидкости, определяемых силами вязкости, и уравнение (1.11) примет вид

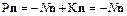
или

.

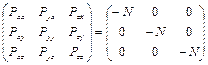Из приведенного уравнения видно, что в статике на поверхностях, ограничивающих бесконечно малый объем жидкости, действуют только нормальные напряжения, причем все они равны между собой. Общее значение нормальных напряжений в данной точке жидкости, взятое с отрицательным знаком, называют гидростатическим давлением p.

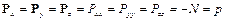. (1.21)

Изотропность (равенство по всем направлениям) нормальных напряжений в неподвижной жидкости называют законом Паскаля.

Этот закон является основой для расчетов всевозможных гидравлических усилителей (гидравлических прессов, гидравлических домкратов и т.п.).