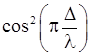Ширина интерференционной полосы
Из (2.5) следует, что в точке 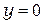 расположен максимум, соответствующий нулевой разности хода. Для него порядок интерференции
расположен максимум, соответствующий нулевой разности хода. Для него порядок интерференции 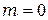 . Это центр интерференционной картины. При переходе к соседнему максимуму
. Это центр интерференционной картины. При переходе к соседнему максимуму 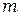 меняется на единицу и
меняется на единицу и 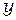 — на величину
— на величину 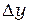 .Расстояние между двумя соседними максимумами (или минимумами)
.Расстояние между двумя соседними максимумами (или минимумами) 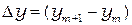 называетсяшириной интерференционной полосы.Из формулы (2.5) или (2.6) легко получить:
называетсяшириной интерференционной полосы.Из формулы (2.5) или (2.6) легко получить:
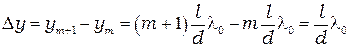 .
.
Отсюда следует, что ширина интерференционной полосы определяется выражением:
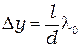 (2.7)
(2.7)
Согласно формуле (2.7), расстояние между полосами растёт с уменьшением расстояния между щелями 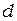 и с увеличением расстояния до экрана
и с увеличением расстояния до экрана 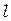 . При
. При 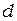 , сравнимом с
, сравнимом с 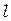 , расстояние между полосами было бы одного порядка с
, расстояние между полосами было бы одного порядка с 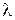 , и составляло бы несколько десятка мкм. В этом случае отдельные полосы были бы совершенно неразличимы, поскольку разрешающая способность глаза ≈ 0,1мм, а длина волны света ≈ 0,5мкм, т.е. на три порядка меньше. Для того чтобы интерференционная картина стала отчётливой, необходимо соблюдение упоминавшегося выше условия
, и составляло бы несколько десятка мкм. В этом случае отдельные полосы были бы совершенно неразличимы, поскольку разрешающая способность глаза ≈ 0,1мм, а длина волны света ≈ 0,5мкм, т.е. на три порядка меньше. Для того чтобы интерференционная картина стала отчётливой, необходимо соблюдение упоминавшегося выше условия 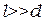 .
.
Период, положение и контрастность интерференционных полос зависят от основных параметров источников излучения: их длины волны (или частоты), начальной фазы, соотношения амплитуд, а также от взаимного расположения источников. Проследим это влияние на модельных экспериментах.
Влияние расстояния между источниками излучения на интерференционную картину продемонстрировано на рис. 2.5.
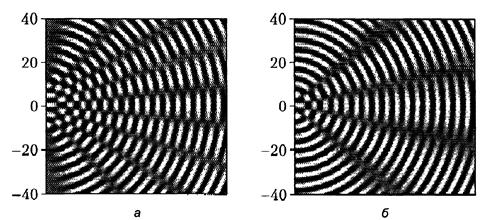
Рис. 2.5. Влияние расстояния между источниками на ширину интерференционных полос: в случае (а) расстояние в два раза больше, чем в случае (б).
На этом рисунке полосы от двух точечных источников в области чередования тёмных и светлых участков (гребней и впадин волн) соответствуют максимумам интерференционной картины, а расходящиеся веером серые полосы — интерференционным минимумам. Как и следует из формулы для ширины интерференционной полосы (2.7), при сближении источников (рис. 2.5б) период интерференционной картины возрастает.
Изменение длины волны источников моделируется на рис. 2.6. При неизменном расстоянии между ними с увеличением длины волны (рис. 2.6б) ширина интерференционной полосы возрастает, чтобы набрать прежнюю разность хода, теперь нужно большее расстояние.

Рис. 2.6. Влияние длины волны на ширину интерференционных полос:
в случае (а) длина волны в два раза меньше, чем в случае (б).
Введём в рассмотрение угол 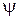 - угол, под которым видны щели S1 и S2 из центра интерференционной картины. Из рис. 2.7 видно, что
- угол, под которым видны щели S1 и S2 из центра интерференционной картины. Из рис. 2.7 видно, что 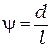 , поэтому формулу для ширины интерференционной полосы (2.7) можно переписать в виде:
, поэтому формулу для ширины интерференционной полосы (2.7) можно переписать в виде:
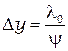 . (2.8)
. (2.8)
|
| |
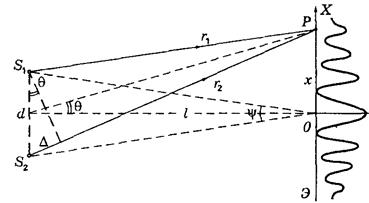
Рис. 2.7
Таким образом, ширина интерференционной полосы пропорциональна длине волны  и обратно пропорциональна углу, под которым видны источники волн из центра интерференционной картины.
и обратно пропорциональна углу, под которым видны источники волн из центра интерференционной картины.
2.2. Распределение интенсивности
Рассмотрим идеализированный случай, когда два одинаковых источника 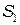 и
и 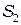 в опыте Юнга строго монохроматические. В интересующую нас точку экрана колебания от этих источников будут приходить практически с одинаковой амплитудой
в опыте Юнга строго монохроматические. В интересующую нас точку экрана колебания от этих источников будут приходить практически с одинаковой амплитудой  . Тогда согласно формуле (1.3)
. Тогда согласно формуле (1.3)
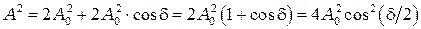 , (2.9)
, (2.9)
где 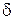 — разность фаз. Последнее выражение записано, используя формулу половинного угла из тригонометрии
— разность фаз. Последнее выражение записано, используя формулу половинного угла из тригонометрии  .
.
Разность фаз согласно формуле (1.14) равна 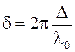 .
.
Поскольку интенсивность 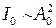 , из (2.8)получим:
, из (2.8)получим:
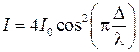 , (2.10)
, (2.10)
где  - порядок интерференции.
- порядок интерференции.
|
 при значении
при значении 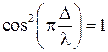 , а в минимумах
, а в минимумах 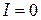 при
при 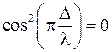 . При отсутствии интерференции
. При отсутствии интерференции 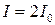 , так как
, так как 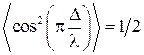
|
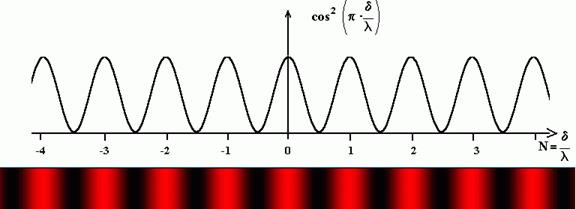
Рис. 2.8. Распределение интенсивности на интерференционной картине
от двойной щели в случае монохроматической волны.
Естественно, что показанное на рис. 2.8 идеализированное распределение интенсивности 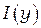 существенно отличается от реального. Эти отличия обусловлены: во-первых, степенью монохроматичности и степенью пространственной когерентности используемого света, и, во-вторых, дифракционными явлениями.
существенно отличается от реального. Эти отличия обусловлены: во-первых, степенью монохроматичности и степенью пространственной когерентности используемого света, и, во-вторых, дифракционными явлениями.
В случае белого света интерференционная картина от двойной щели представляет собой чередование тёмных и разноцветных полос, параллельных друг другу (Рис. 2.9.).
Центральная полоса или нулевой максимум ( 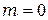 ) белого цвета, поскольку соответствует нулевому сдвигу фаз для всех компонент белого света. Остальные максимумы разложены в спектр. Но, начиная со второго максимума, интерференционные полосы перекрываются и далее исчезают.
) белого цвета, поскольку соответствует нулевому сдвигу фаз для всех компонент белого света. Остальные максимумы разложены в спектр. Но, начиная со второго максимума, интерференционные полосы перекрываются и далее исчезают.

Рис. 2.9.
Появление разноцветных полос, очевидно, связано с тем, что условия интерференции (1.16 и 1.18) для различных частотных компонентов белого света соблюдаются в пространственно различных точках экрана (  и
и 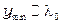 ). Чем больше длина волны, тем дальше от центра располагается максимум или минимум для данной длины волны.
). Чем больше длина волны, тем дальше от центра располагается максимум или минимум для данной длины волны.
Из формулы ширины интерференционной полосы (2.7) следует, что:
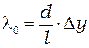 . (2.11)
. (2.11)
Измерив, расстояние между полосами 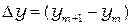 , а также расстояние от щелей до экрана
, а также расстояние от щелей до экрана 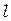 и расстояние между центрами щелей
и расстояние между центрами щелей 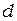 можно вычислить
можно вычислить  . Именно из опытов по интерференции света впервые Юнгом были определены длины волн для световых лучей разного цвета.
. Именно из опытов по интерференции света впервые Юнгом были определены длины волн для световых лучей разного цвета.
Дата добавления: 2015-01-21; просмотров: 21212;