ПОЛОСЫ РАВНОЙ ТОЛЩИНЫ
Клиновидные пластинки. Пусть стеклянная пластинка имеет форму клина с углом раствора 
, и на неё падает плоская монохроматическая световая волна. Теперь отражённые от поверхностей клина световые волны будут распространяться не в одном направлении, а под некоторым углом (рис. 5.1). Выясним, прежде всего, где будет локализована интерференционная картина. Это проще всего сделать с помощью рис. 5.2, на котором показано, что происходит с областью когерентности после расщепления волны при отражении от поверхностей клина.
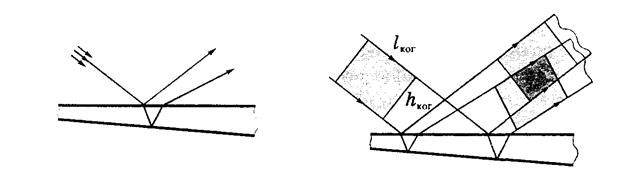
Рис.5.1 Рис. 5.2
Из рисунка видно, что при небольших значения длины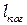 
и ширины 
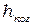когерентности область перекрытия когерентных частей отраженных волн локализована, в основном, вблизи поверхности клина. Это область становится все более узкой по мере перемещения в сторону утолщения клина, постепенно исчезая совсем.
Так как разность хода лучей, отразившихся от различных участков клина, неодинакова, в области локализации интерференции появятся светлые и темные полосы, параллельные ребру клина. Каждая из таких полос возникает в результате отражений от участков клина с одинаковой толщиной, поэтому их называют полосами равной толщины. Локализованные вблизи поверхности клина интерференционные полосы можно наблюдать непосредственно глазом, фокусируя его на поверхность клина, либо с помощью линзы, сфокусированной также на поверхность клина. С помощью линзы интерференционную картину с поверхности клина можно отобразить на экран Э, расположенный в плоскости, сопряженной с поверхностью клина.
Полосы равной толщины можно наблюдать в тонкой клиновидной прослойке воздуха между поверхностями двух прозрачных пластинок. Если направление наблюдения близко к нормальному, то оптическая разность хода лучей, отраженных от поверхностей клина в месте, где ширина зазора равна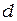 
, определяется как 
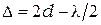. Там, где 
, 
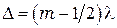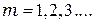, возникают минимумы. Т. е. тёмные полосы возникают в тех местах, где толщина зазора 
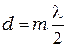. Переход от одной полосы к соседней соответствует изменению толщины зазора на 
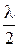. Каждая полоса соответствует определенной толщине зазора. Этот факт используют для проверки качества оптических поверхностей при их шлифовке, наблюдая в отраженном свете прослойку между контролируемой и эталонной поверхностями. Измеряя ширину полосы 
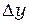в монохроматическом свете с известной длиной волны 
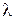, можно измерить углы порядка 0,1 угл. мин и меньше.
В предыдущих рассуждениях мы принимали во внимание только волны, отраженные от поверхностей воздушного клиновидного зазора, игнорируя волны, отраженные от наружных поверхностей пластинок. Это можно сделать лишь постольку, поскольку толщина пластинок обычно значительно превышает длину когерентности используемого света от обычных источников, и отраженные от этих поверхностей волны оказываются некогерентными.
5.1. Кольца Ньютона
Кольца Ньютона – это классический пример кольцевых полос равной толщины, наблюдаемых при отражении света от поверхностей зазора между стеклянной пластинкой и соприкасающейся с ней выпуклой линзой(рис. 5.3).
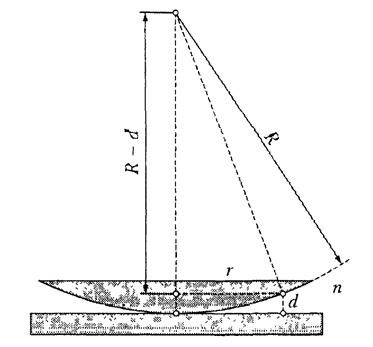
Рис. 5.3
Волна, отражённая от верхней поверхности линзы, в силу небольшойдлины когерентности обычных источников света, не когерентна с волнами, отражёнными от поверхностей зазора и участия в образовании интерференционной картины не принимает. Поэтому мы её и не будем учитывать.
Из-за радиальной симметрии линзы полосы равной толщины при нормальном падении света имеют вид концентрических окружностей с центром в точке соприкосновения. При наклонном падении – эллипсов. Интерференцию можно наблюдать и в проходящем свете, причём в проходящем свете максимумы интерференции соответствуют минимумам интерференции в отражённом свете и наоборот.
Найдем радиусы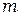 
-ных тёмных колец (минимумов). Сначала запишем условие образования тёмных колец. Они возникают там, где оптическая разность хода волн 
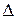, отражённых от обеих поверхностей зазора, равна нечётному числу полуволн (условие минимума 
).
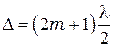В случае нормального падения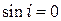 
и формулы (4.2) следует, что в отражённом свете оптическая разность хода:
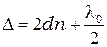, (5.1).
где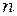 
- абсолютный показатель преломления материала зазора (жидкость или воздух).
Выразим величину зазора 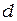через радиус линзы 
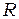и радиус тёмного интерференционного кольца 
.
.
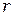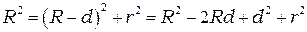
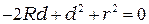С учетом того, что 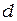мало, можно пренебречь 
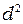по сравнению с 
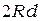. Отсюда
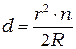. (5.2)
Подставим (5.2) в (5.1) и применим условие минимума. Получим
.
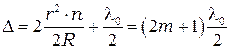Отсюда радиусы тёмных колец:
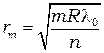
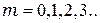(5.3)
Аналогичный расчёт можно провести для светлых колец. Радиусы светлых колец:
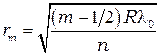
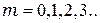(5.4)
Заметим, что значению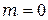 
соответствует минимум тёмного пятна (не кольца).
Следует обратить внимание на то, что формулы (5.3) и (5.4) справедливы лишь в случае идеального (точечного) контакта сферической поверхности линзы с пластинкой. Но идеальных контактов не бывает, поэтому номера колец не равны, вообще говоря, порядку интерференции 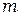, и это обстоятельство необходимо учитывать при расчётах.
Если линзу постепенно отодвигать от поверхности пластинки, то интерференционные кольца будут стягиваться к центру: это ведь кольца (полосы) равной толщины, а она при этом перемещается к центру. С помощью колец Ньютона можно с достаточно высокой точностью контролировать качество изготовления, например, сферических поверхностей.
Рассмотрим теперь на конкретном примере вопрос, связанный с причиной локализации колец Ньютона в очень малой области для обычных линз (кольца приходится рассматривать в микроскоп).
Пусть двояковыпуклая линза, радиус кривизны сферической поверхности которой 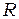= 60мм, соприкасается со стеклянной пластинкой. Оценим радиус наблюдаемой в отраженном свете интерференционной картины, если длина волны света 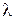= 0,60 мкм и 
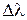=0,06 мкм. Свет падает практически нормально.
При нормальном падении света ограничивать интерференционную картину будет только длина когерентности 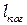. Кольца исчезают, когда разность хода волн становится равной длине когерентности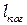
,
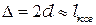где 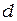— ширина зазора в месте исчезновения колец. Согласно формуле (5.2) ширина зазора 
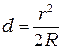, а длина когерентности 
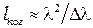из (3.3).Из этих формул получим 
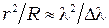, откуда максимальный радиус видимого кольца
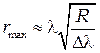=0,6 мм.
Отсюда следует, что при обычных размерах линз интерференционную картину необходимо рассматривать в микроскоп.
Максимальное число видимых колец, согласно (3.2), равно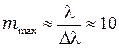 
. Этот результат можно получить и из формулы (5.3).
6. ИНТЕРФЕРОМЕТРЫ И ИНТЕРФЕРОМЕТРИЯ
Интерферометрия – это оптические измерения с использованием явления интерференции. Как правило, это тонкие и точные измерения, выполняемые на специальных приборах - интерферометрах. В качестве интерферометра могут использоваться установки, собранные для наблюдения и изучения интерференции.
Условие (1.16) максимума интерференции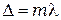 
включает длину волны излучения, показатели преломления сред, в которых распространяется излучение, и длину хода лучей, определяемую геометрическими параметрами установки. Определяя положение или смещение максимумов и минимумов интерференционной картины, можно соответственно определить:
а) длину волны излучения;
б) показатели преломления, их изменение, а также другие параметры среды, влияющие на показатель преломления, например, давление газа или состав газовой смеси;
в) малые или не малые размеры (например, можно воссоздать эталон метра), перемещения, деформации, скорости и т.д. Наиболее распространены интерферометры Майкельсона, Линника, Маха-Цендера, Фабри-Перо, Релея, Жамена. Для нестандартных измерений разрабатывают специальные интерферометрические схемы.
7. ОСНОВНОЙ ПРИНЦИП ИНТЕРФЕРЕНЦИОННЫХ СХЕМ
Интерференция характерна для волн любой природы и сравнительно просто наблюдается на опыте для волн на поверхности воды или для звуковых волн. Наблюдать же интерференцию световых волн можно лишь при определенных условиях. Рассмотренные выше примеры интерференции являются идеализированными, так при интерпретации предполагалось, что источник света является точечным и излучает монохроматические сферические или плоские волны. Поэтому эти результаты имеют ограниченную применимость, так как реальные источники света не являются таковыми.
Дело в том, что свет, испущенный обычными (не лазерными) источниками, не бывает монохроматическим. Такой свет можно рассматривать как хаотичную последовательность отдельных цугов синусоидальных волн, длительность отдельного цуга порядка 10-8с, поэтому при наложении световых волн от разных источников фазовые соотношения между световыми колебаниями многократно изменяются случайным образом. Источники оказываются некогерентными, и достаточно устойчивой картины интерференции не возникает (сменяющие друг друга с весьма большой частотой картины интерференции в дальнейшем нас интересовать не будут, их регистрация требует специальных малоинерционных приемников). Поэтому для наблюдения интерференции с использованием немонохроматического света приходится прибегать к различным ухищрениям: применять спектральные фильтры, располагать источники таким образом, чтобы их можно было считать точечными и другим. И, тем не менее, когерентные световые волны можно получить даже от обычных источников. Общий принцип их получения таков: волну, излучаемую одним источником света, разделяют тем или иным способом на две части и затем накладывают их друг на друга подходящим способом.
Если разность хода этих волн от источника до точки наблюдения не превышает некоторые характерные длины, то случайные изменения амплитуды и фазы световых колебаний в двух волнах происходят согласованно (когерентно), и мы будем наблюдать интерференционную картину, например, систему чередующихся светлых и темных полос.
Как было показано ранее, образовавшиеся после разделения волны во всех интерференционных схемах можно представить как бы исходящими из двух точечных источников(действительных или мнимых — это не существенно).
Способы разделения волны от первичного источника на две когерентные между собой волны можно разбить на две группы: деление волнового фронта и деление амплитуды. На рис. 6.1приведены примеры нескольких интерференционных схем, широко применяемых на практике.
Схемы на рис. 6.1 а-г относятся к первой группе. Во всех схемах излучение источника S попадает на экран по двум различным путям (плечам) интерференционной схемы, отмеченным на рисунках индексами 1 и 2. В любом случае вместо первичного источника можно рассматривать два когерентных источника S1 и S2, находящихся на некотором расстоянии d. Для определения положения и формы интерференционных полос излучение можно считать монохроматическим. Наиболее важными характеристиками любой интерференционной схемы являются: угол схождения волны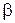 
в точке наблюдения и угол между лучами, исходящими из источника S, которые каким-либо способом сводятся далее в точку наблюдения. Угол 
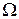называется апертурой интерференции.
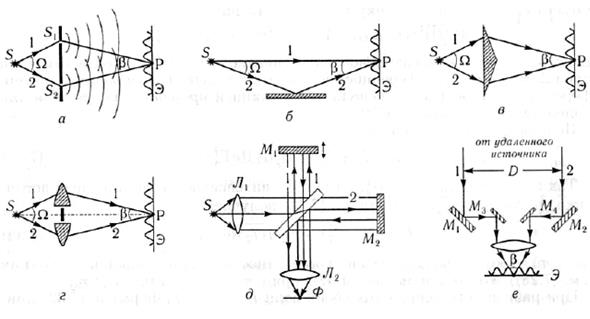
Рис. 6.1. Некоторые интерференционные схемы, широко применяемые в оптике: а — схема Юнга, б — схема Ллойда, в — бипризма Френеля, г — билинза Бийе, д — интерферометр Майкельсона, е — звёздный интерферометр. Все лучи 1 и 2 идут от удалённого источника.
Две когерентные световые волны можно получить в результате отражения света от двух поверхностей плоскопараллельной прозрачной пластинки (пленки) (Рис. 6.1г). В каждую точку наблюдения приходят волны, разность хода которых будет такой же, как от источников S1 и S2 — изображений S, создаваемых верхней и нижней поверхностями. Интерференционные полосы на экране B будут иметь вид концентрических колец с центром в точке O. При точечных источниках света будут наблюдаться резкие интерференционные картины при любом положении экрана, пересекающего интерференционные полосы. Такие полосы интерференции называют нелокализованными.
При плавном изменении разности хода интерферирующих пучков на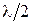 
интерференционная картина сместится настолько, что на месте максимумов окажутся минимумы. Поэтому явление интерференции используют в интерферометрах для измерения длины тел, длины световой волны, изменения длины тела при изменении температуры, сравнимых с .
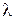Дата добавления: 2015-01-21; просмотров: 5298;