ПОЛОСЫ РАВНОГО НАКЛОНА

Рассмотрим интерференцию в тонких пластинках. Пусть из воздуха ( 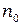= 1) на плоскопараллельную прозрачную пластинку с показателем преломления 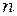и толщиной 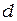под углом 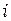падает плоская монохроматическая волна (рис.4.1а).

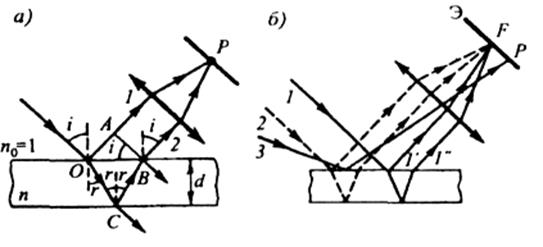
Рис. 4.1

В точке О луч частично отразится (1), а частично преломится и, после отражения на нижней поверхности пластины в точке С, выйдет из пластины в точке В (2). Вообще, в случае плоской пластинки будет наблюдаться многократное отражение и преломление от внутренних поверхностей пластинки, но мы этим пренебрежём из-за слабой интенсивности этих многократно отражённых лучей. Лучи 1 и 2 параллельны и с помощью собирающей линзы их можно свести в точке Р.

Необходимо отметить важную особенность отражения электромагнитных волн (и в частности, оптических лучей) при падении их на границу раздела двух сред из среды с меньшей диэлектрической проницаемостью. При отражении света от более плотной среды ( 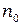< 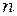) фаза изменяется на 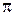. Изменение фазы на 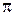равносильно потере полуволны при отражении.

Такое поведение электромагнитной волны на границе двух сред следует из граничных условий, которым должны удовлетворять тангенциальные компоненты векторов напряженности электрического и магнитного поля на границе раздела: 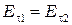, 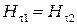. С учетом этого оптическая разность хода:

.

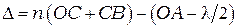Из рис. 4.1 видно, что 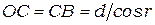и

.

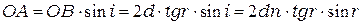Последнее выражение записано, используя закон преломления .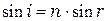

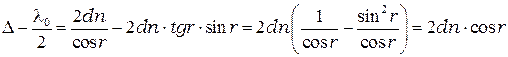
или

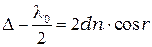. (4.1)

Так как 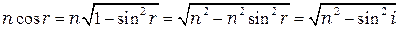, то в итоге получаем формулу, определяющую разность хода между отражённой и преломлённой волной на тонкой пластинке:

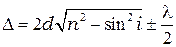. (4.2)

Если отражённые волны 1 и 2 (рис. 4.1б)когерентны между собой, то в точке наблюдения 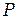будут наблюдаться максимумы отражения при условии:

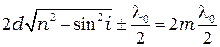. (4.3)

В точке 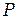будет интерференционный минимум, если

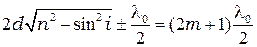, (4.4).

где 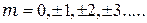- целое число (порядок интерференции).

Меняя угол падения, мы будем наблюдать последовательную смену максимумов и минимумов отражения. (Заметим, что при минимуме отражения наблюдается максимум проходящего через пластинку света, и наоборот.) Если бы обе отражённые волны были некогерентными, то такого явления мы не наблюдали бы: по мере увеличения угла падения интенсивность отраженного света монотонно уменьшалась бы.

Теперь выясним условия, при которых отражённые волны будут когерентными и смогут интерферировать. В предыдущем разделе мы установили, что для этого должны выполняться соотношения между длиной когерентности и разностью хода:

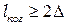(3.6)

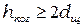. (3.7)

Здесь 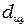- расстояние между щелями в опыте Юнга, т.е. источниками вторичных волн. Для нашего случая под 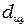нужно понимать поперечное смещение между отражённым и преломлённым лучами (расстояние AB на рис.4.1).

Проиллюстрируем ситуацию с помощью рис. 4.2. Выделим в падающей волне некоторую область когерентности 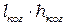(она слегка затенена на рисунке) и проследим за её дальнейшей судьбой. После расщепления падающей волны расщепится и выделенная область когерентности, причем так, что в отражённых волнах эти области когерентности сместятся относительно друг друга (рис.4.2а). Если они при этом перекрываются (на рисунке более тёмный участок), интерференция будет наблюдаться и тем более отчетливо, чем больше степень перекрытия.

Нетрудно заметить, что для пластинки с большей толщиной область перекрытия когерентных участков уменьшается (рис. 4.2б), и интерференция будет наблюдаться все менее отчетливо. Начиная с некоторой толщины пластинки, интерференция исчезнет совсем.

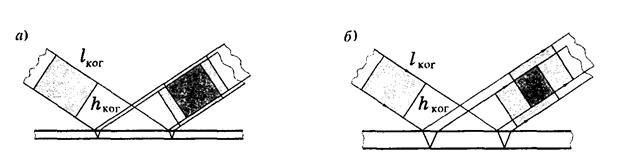
Рис. 4.2

Из рис. 4.2 видно, что смещение расчленённых частей области когерентности происходит как вдоль распространения волны (оно не должно превосходить длину когерентности 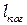), так и поперёк распространения волны (смещение не должно превосходить ширину когерентности 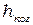). Интерференция будет наблюдаться лишь в том случае, когда будут удовлетворены оба эти условия. Напомним, что для лучшей видимости мы договорились брать половины значени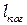й и 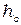. Перейдем к расчёту. Согласно (3.6) 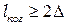, необходимо, чтобы оптическая разность хода 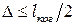. Следовательно,

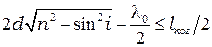.(4.5)

Для оценки необходимого значения толщины пластинки 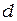будем считать, что корень в этом выражении равен величине порядка единицы (что обычно и бывает), а также пренебрежем 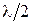. Тогда получим

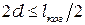, (4.6)

т. е. необходимо, чтобы удвоенная толщина пластинки была не более половины длины когерентности используемого излучения. Например, если 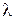= 600 нм, а 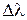= 3 нм, то толщина пластинки

.

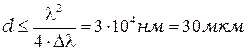Далее, поперечный сдвиг частей области когерентности не должен превосходить половины ширины когерентности 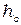. Этот сдвиг, как видно из рис. 4.1, равен отрезку АВ. Значит, необходимо, чтобы 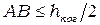.Из рис. 4.1 следует, что

.

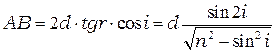Видно, что это смещение существенно зависит от угла падения 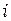. Чем меньше угол падения, тем меньше смещение 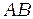, тем меньше может быть 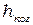. И основную роль в этом случае будет играть длина когерентности. При 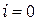смещение происходит только вдоль распространения волн, поперёк — оно равно нулю, и ширина когерентности 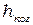, становится практически не существенной.

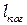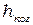Обратимся к вопросу, что следует понимать под словами тонкая пластинка. Когда говорят, что интерференция происходит при отражении от тонкой пластинки, то имеют в виду, что её толщина (в той или иной степени) меньше и (если 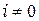). Причем — это важно — при нормальном падении интерференция обеспечивается только соотношением между толщиной пластинки и 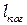. Для солнечного света ( 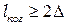) пластинка будет тонкой, если ее толщина порядка нескольких длин волн. Длину когерентности можно увеличить с помощью светофильтров, соответственно увеличивается и толщина пластинки, которую мы называем тонкой. Для лазерного же излучения тонкой будет пластинка в десятки сантиметров и метров (в зависимости от длины когерентности излучения используемого лазера).

Из формул (4.3) и (4.4) следует, что при падении плоской световой волны на плоскопараллельную тонкую пластинку интенсивность отражённого света зависит от угла падения. Изменяя этот угол, мы будем наблюдать чередование максимумов и минимумов отражённого света. Это можно использовать для получения интерференционной картины в виде привычной системы полос. Достаточно использовать в качестве падающего рассеянный монохроматический свет (он содержит волны, падающие на пластинку одновременно под разными углами), а на пути отраженного света поставить линзу и в ее фокальной плоскости экран (рис.4.3).

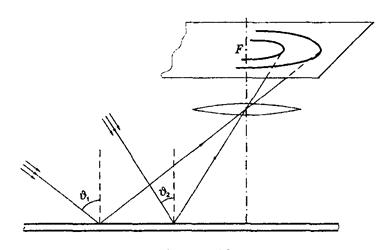
Рис. 4.3

Максимумы на экране будут располагаться в местах, соответствующих условию (4.3)

.

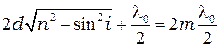Полоса данного порядка интерференции обусловлена светом, падающим на пластинку под одним и тем же углом 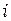, но с разных направлений. Поэтому такие полосы называют полосами равного наклона. При расположении линзы как показано на рис. 4.3, эти полосы имеют вид концентрических колец с центром в ее фокусе F.

Порядок интерференции 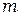растёт с уменьшением угла падения 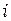, и в центре картины он максимален.Поскольку для наблюдения интерференционной картины в данном случае экран помещают в фокальной плоскости линзы, т. е. так, как его располагают для получения на нем изображения бесконечно удаленных предметов, то говорят, что полосы равного наклона локализованы в бесконечности. Роль линзы и экрана может играть хрусталик и сетчатка глаза. В этом случае для наблюдения полос равного наклона глаз нужно аккомодировать (настраивать) так, как при рассмотрении удаленных предметов.

В белом свете интерференционные полосы окрашены. Поэтому такое явление называют цвета тонких пластинок.