ОПЫТ ЮНГА. РАСЧЁТ ИНТЕРФЕРНЦИОННОЙ КАРТИНЫ ОТ ДВУХ ЩЕЛЕЙ
В оптике явление интерференции впервые наблюдалось Юнгом в 1801 г. (рис. 2.3). Здесь свет от источника проходит сначала через маленькое отверстие в экране S, а затем падает на другой экран с двумя маленькими отверстиями S1 и S2, разнесенными на некоторое расстояние 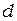 . Прошедший через отверстия свет падает на экран Э, где и наблюдается интерференционная картина. Опыт Юнга был первым убедительным доказательством того, что наложение света может образовать темноту, а наблюдение интерференции в опыте Юнга явилось экспериментальным доказательством волновой природы света.
. Прошедший через отверстия свет падает на экран Э, где и наблюдается интерференционная картина. Опыт Юнга был первым убедительным доказательством того, что наложение света может образовать темноту, а наблюдение интерференции в опыте Юнга явилось экспериментальным доказательством волновой природы света.
|
|
| |||
| |||
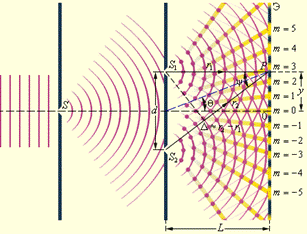
Когерентные световые волны можно получить, разделив (с помощью отражений или преломлений) волну, излучаемую одним источником, на две части. Если потом заставить эти две волны пройти разные оптические пути, а потом наложить друг на друга, наблюдается интерференция. Разность оптических длин путей, проходимая интерферирующими волнами, не должна быть очень большой, так как складывающиеся колебания должны принадлежать одному и тому же результирующему цугу волн.
|
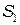 и
и 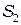 , имеющих вид светящихся точек или щелей, расположенных на расстоянии
, имеющих вид светящихся точек или щелей, расположенных на расстоянии 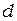 (Рис. 2.4). Экран Э параллелен щелям и находится от них на расстоянии
(Рис. 2.4). Экран Э параллелен щелям и находится от них на расстоянии 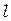 , при этом
, при этом 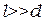 . Область, в которой волны перекрываются, называется полем интерференции.
. Область, в которой волны перекрываются, называется полем интерференции.
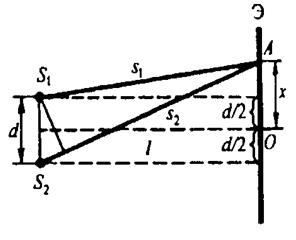
Найдём положение максимумов и минимумов на интерференционной картине от двух щелей. Интенсивность в произвольной точке А, находящейся на расстоянии 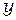 от центра интерференционной картиныв точке О , определяется разностью хода двух волн:
от центра интерференционной картиныв точке О , определяется разностью хода двух волн:
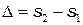 . (2.1)
. (2.1)
Из геометрических построений на рис. 2.4 видно, что:
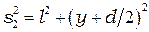 , (2.2)
, (2.2)
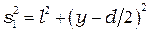 .
.
Вычитая из первого уравнения второе и пренебрегая членом 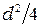 , получим:
, получим:
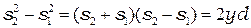 .
.
Отсюда:
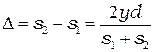 . (2.3)
. (2.3)
Из условия 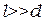 следует
следует 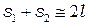 , поэтому оптическая разность хода в точке А равна:
, поэтому оптическая разность хода в точке А равна:
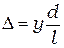 . (2.4)
. (2.4)
Подставив выражение для разности хода (2.4) в условие наблюдения максимума (1.16) и минимума (1.18), получим выражение для расстояний от центра 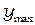 и
и 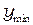 для максимумов и минимумов интенсивности света:
для максимумов и минимумов интенсивности света:
положение максимумов при 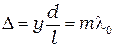 отсюда:
отсюда:
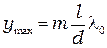 (
( 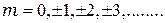 ), (2.5)
), (2.5)
положение минимумов при 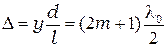
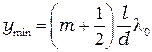 (
( 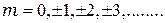 ). (2.6)
). (2.6)
Дата добавления: 2015-01-21; просмотров: 5180;
