Введение. Электромагнитная природа света

Интеллект ..............

Природа интеллекта .........

Структура интеллекта ........

Истоки интеллекта .........

Оценка интеллекта .........

Интеллект, решение проблем и творчество .

Творческое мышление

Особенности творческого мышления

Творчество и адаптация ..............

Особенности творческих личностей .........

Документ 9.1. IQ: два ребенка- это хорошо, а девять – это, наверное, многовато . . ..........

Документ 9.2. Какая нужна школа и для кого? .....

Документ 9.3. Следует ли отказаться от тестов на умствен­ное развитие? ..................

Документ 9.4. «Нормальный» и «аномальный» интеллект

Документ 9.5. Интеллект и творчество; ребенок, особенно­сти его личности и его семья ............

Резюме .....................

Досье 9.1. Является ли интеллект врожденным или приоб­ретенным .....................

Досье 9.2. Интеллект компьютера и интеллект человека . .

Литература ....................

Материал для самопроверки .............

Ответы на вопросы ...............

ВОЛНОВАЯ ОПТИКА

ИНТЕРФЕРЕНЦИЯ

КРАТКАЯ ТЕОРИЯ

Введение. Электромагнитная природа света

В представлениях физической или волновой оптики оптическое излучение или светпредставляет собой электромагнитные волны – это переменное электромагнитное поле, распространяющееся в пространстве с конечной скоростью. Поэтому оптика - это часть общего учения об электромагнитном поле, которая называется электродинамикой, основой которой являются уравнения Максвелла. Из уравнений Максвелла следуют волновые уравнения, решениями которого, в частности, являются уравнения плоской волны:

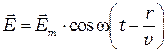(1)

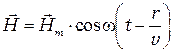
где 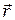- радиус вектор точки с координатам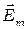и; и 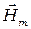- амплитуды колебаний электрического и магнитных полей; 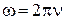- циклическая частота; 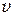- фазовая скорость волны. Уравнения (1) описывают поведение векторов 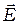и 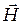как во времени так в пространстве. Таким образом, Максвеллом было теоретически предсказано существование электромагнитных волн. Экспериментальное подтверждение возникновения электромагнитных волн выполнено Г. Герцем, который первым осуществил генерацию и приём электромагнитных волн и исследовал их свойства.

Обычно уравнение плоской волны записывают в виде:

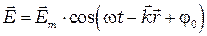(2)

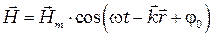
где 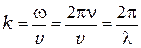- волновое число; 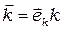- волновой вектор, где 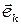- единичный вектор нормали к волновому фронту совпадающий с направлением скорости .

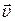Величина, стоящая под знаком косинуса 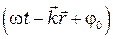- называется полной фазой волны, 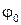- начальная фаза колебаний. Фазу 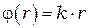, связанную с изменением расстояния 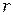пройденного волной, называют набегом фазы или фазовым сдвигом.

Уравнение 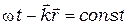определяет в пространстве поверхность с одинаковыми фазами волн. Эта поверхность или геометрическое место точек с одинаковым значением фаз называется волновой поверхностью. Для плоской гармонической волны волновая поверхность это плоскость. Для сферической волны испускаемой точечным источником – это сфера. В обоих случаях волновой вектор 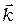перпендикулярен волновой поверхности.

Из анализа уравнений Максвелла и его решений в виде (1) следует, что электромагнитные волны имеют следующую структуру:

1. Электромагнитные волны - это поперечные волны. Векторы 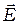и 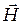напряжённостей электрического и магнитных полей волны взаимно перпендикулярны и колеблются в плоскости перпендикулярной вектору скорости ( ).

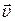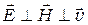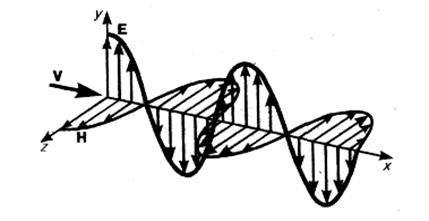
Рис. 1. Структура плоской электромагнитной волны.

2. Векторы 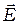, 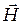и 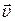образуют правовинтовую систему и всегда колеблются в одинаковых фазах (рис. 1).

3. Мгновенные значения векторов 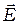и 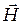(модули векторов) в любой точке связаны соотношением:

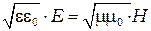(3)

Поток энергии переносимый электромагнитной волной характеризуется вектором Пойтинга 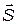, который определяемый векторным произведением векторов 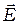и :

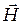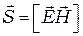. (4)

Вектор 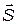также направлен по нормали к волновому фронту в сторону распространения электромагнитных волн.

Плотность потока электромагнитной энергии или интенсивность света определяется усреднённым по времени модулем вектором Пойтинга 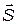, причём время усреднения .

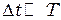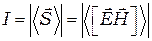(5)

Так как 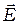и 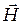взаимно перпендикулярны, векторное равенство можно заменить скалярным 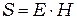. Согласно формулы (3) 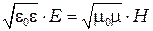, отсюда:

,

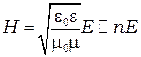поэтому формулу (5) можно записать так:

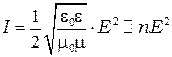(6)

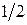( появилась в результате усреднения квадрата косинуса)

Положив 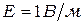, 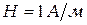получим единицу вектора Пойтинга .

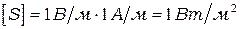Оптические свойства среды, в которой распространяется свет, характеризуются величиной, называемой абсолютным показателем преломления .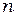

Определение. Абсолютный показатель преломленияпоказывает во сколько раз скорость света в вакууме 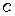больше скорости света в веществе:

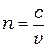. (7)

Относительный показатель преломления одной среды по отношению к другой равен отношению абсолютных показателей преломления этих сред:

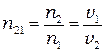(8)

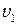где и 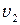- фазовая скорость света в первой и во второй среде соответственно.

Поскольку при распространении в веществе скорость света уменьшается, длины световых волн в веществе будут иными, чем в вакууме. В среде с абсолютным показателем преломления 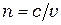фазовая скорость световой волны 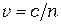. Длиной волны света называется величина 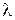. По определению, это расстояние на которое распространяется колебание за время равное одному периоду, т.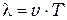е. , где 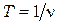- период колебания, 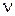- частота колебаний. Тогда в среде длина волны имеет значени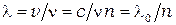е , где 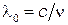- длина волны света в вакууме. Таким образом, длина световой волны в среде с показателем преломления 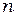связана с длиной волны в вакууме соотношением:

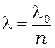(9)

Согласно электромагнитной теории света Максвелла:

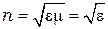, (10)

что справедливо для подавляющего большинства прозрачных веществ с .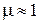

Последняя формула связывает оптические свойства вещества с его электрическими свойствами. Заметим, что 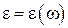зависит от частоты электромагнитной волны. Этим объясняется дисперсия света, т. е. зависимость 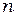(или 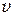) от частоты (или длины волны).

Показатель преломления 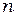характеризует оптическую плотность среды. Среду с большим показателем преломления называют оптически более плотной.

Поскольку фазовая скорость зависит от показателя преломления, для описания распространения световых волн в различных средах вводится понятие оптический путь 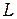, определяемый произведением геометрического пути 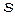на показатель преломления:

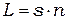. (11)

При наложении двух волн одинаковой частоты прошедших разные оптические пути между ними возникает оптическая разность хода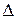

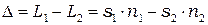. (12)

Оптическая разность хода основная физическая величина, используемая в теории построения оптических изображений.