Системы линейных алгебраических уравнений (СЛАУ).

Основные понятия.

Опр. Система линейных алгебраических уравнений (СЛАУ), состоящая из m уравнений с n неизвестными x₁, …, x_n имеет следующий вид

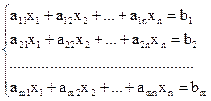, (4.1)

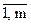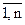где числа a_ij (i = ; j = ) - называются коэффициентами СЛАУ, а b_i – свободными членами СЛАУ, причем (a_ij, b_i)ÎR. При этом индекс i обозначает номер уравнения, а индекс j – номер неизвестной.

NB. Система алгебраических уравнений называется линейной, если все уравнения системы содержат неизвестные только в первой степени, причем они между собой не перемножаются.

СЛАУ называется квадратной, если в ней число уравнений равно числу неизвестных, то есть m = n.

СЛАУ называется однородной, если все ее свободные члены равны нулю, то есть "b_i=0 (i = ).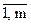

СЛАУ называется неоднородной, если среди ее свободных членов хотя бы один не равен нулю, то есть $b_i¹0.

Решением СЛАУ называется такая совокупность значений неизвестных x₁= C₁, x₂= C₂,…, x_n = C_n, которая каждое уравнение СЛАУ обращает в верное числовое равенство (тождество).

СЛАУ называется совместной, если она имеет хотя бы одно решение, и, соответственно, несовместной, если она вообще не имеет решений.

Совместная СЛАУ называется определенной, если она имеет только одно решение, и неопределенной, если она имеет более одного решения. Неопределенная СЛАУ всегда имеет бесконечное множество решений. Тогда каждое ее решение называется частным решением СЛАУ, а множество всех частных решений называется общим решением СЛАУ.

Две СЛАУ называются эквивалентными, если они имеют одинаковые решения.

Элементарными (тождественными) преобразованиями СЛАУ называются:

1) перестановка уравнений,

2) умножение любого уравнения на число l ¹ 0,

3) прибавление одного уравнения к другому.

NB. При элементарных преобразованиях получаются эквивалентные СЛАУ.

СЛАУ (4.1) кратко записывается в виде матричного уравнения

А×Х = В, (4.2)

где A= - матрица коэффициентов СЛАУ; X= 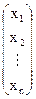- матрица-столбец неизвестных; B= 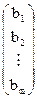- матрица-столбец свободных членов. Кроме того, СЛАУ (4.1) можно записать в виде суммы следующих матриц-столбцов:

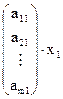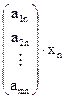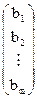+ +…+ = (4.3)