Формулы Крамера для решения квадратной СЛАУ.
Решение квадратной СЛАУ в матричной форме Х = А-1×В запишем в виде
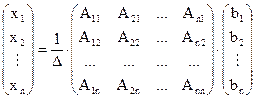 Þ
Þ 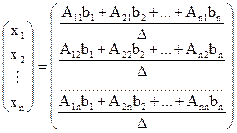 Þ
Þ
Þ x1= 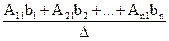 ,
,
………………………………
xn=  ,
,
где A11b1+A21b2+…+An1bn есть разложение по первому столбцу определителя D1:
D1 = 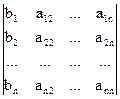 .
.
Определитель D1 называется первым побочным определителем квадратной СЛАУ, который получается из ее главного определителя D заменой 1-го столбца на столбец свободных членов. Следовательно, х1 = 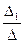 . Аналогично находим, что хn =
. Аналогично находим, что хn =  , где Dn есть n–ый побочный определитель квадратной СЛАУ, который получается из ее главного определителя D заменой n–го столбца на столбец свободных членов. Таким образом, для квадратной СЛАУ значения неизвестных xi находятся по формулам
, где Dn есть n–ый побочный определитель квадратной СЛАУ, который получается из ее главного определителя D заменой n–го столбца на столбец свободных членов. Таким образом, для квадратной СЛАУ значения неизвестных xi находятся по формулам
xi = 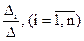 , (4.5)
, (4.5)
где Di есть i–ый побочный определитель квадратной СЛАУ, который получается из ее главного определителя D заменой i–го столбца на столбец свободных членов.
Формулы (4.5) называются формулами Крамера.
Правило Крамера. Если главный определитель квадратной СЛАУ не равен нулю (D¹0), то такая СЛАУ имеет единственное решение в виде (4.5) (т.е. она является совместной и определенной). Если главный определитель квадратной СЛАУ равен нулю (D = 0), то формулы Крамера в виде (4.5) применять нельзя, так как деление на нуль недопустимо. Тогда решение квадратной СЛАУ следует искать в виде
D×xi = Di (4.6)
В этом случае, если хотя бы один из побочных определителей Di ¹ 0 (при D = 0), то такая СЛАУ решений не имеет (то есть она является несовместной), так как при "xi левая часть i–го уравнения (4.6) равна нулю, а правая – нет, то есть равенство (4.6) не выполняется ни при каких значениях хi.
Если же D = D1 = … = Dn = 0, то такая квадратная СЛАУ имеет бесконечное множество решений (то есть является совместной и неопределенной), так как равенства (4.6) выполняются при любых значениях хi.
Пример 1. Решить СЛАУ 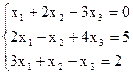
Решение. Это квадратная СЛАУ. Ее главный определитель равен


 D=
D=  -2 =
-2 = 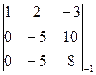 =
= 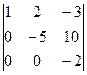 = 10 ¹ 0 Þ данная СЛАУ имеет единственное решение, определяемое формулами Крамера (4.5).
= 10 ¹ 0 Þ данная СЛАУ имеет единственное решение, определяемое формулами Крамера (4.5).


 -2 1
-2 1
 D1 =
D1 =  =
= 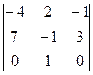 = 1×(-1)5
= 1×(-1)5 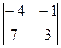 =
= 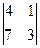 = 12-7 = 5 Þ х1 =
= 12-7 = 5 Þ х1 = 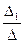 = 0,5.
= 0,5.


 3
3

 D2 =
D2 = 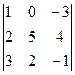 =
=  =1×(-1)2×
=1×(-1)2× 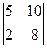 = 5×2×
= 5×2× 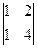 = 10×(4-2) = 20 Þ х2 =
= 10×(4-2) = 20 Þ х2 = 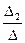 = 2.
= 2.


 -2
-2
 D3 =
D3 = 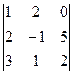 =
= 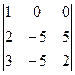 =1×(-1)2×(-5)×
=1×(-1)2×(-5)× 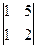 = -5×(2-5) = 15 Þ х3 =
= -5×(2-5) = 15 Þ х3 = 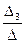 = 1,5.
= 1,5.
Проверка.
0,5+2×2-3×1,5=0 Û 0º0
2×0,5-2+4×1,5=5 Û 5º5
3×0,5+2-1,5=2 Û 2º2
Ответ: х1 = 0,5; х2 = 2; х3 = 1,5.
Пример 2. Решить квадратную СЛАУ 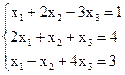


 -2 -1
-2 -1
 Решение: D =
Решение: D = 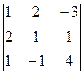 =
= 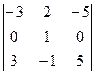 = 1×(-1)4×
= 1×(-1)4×  = 0.
= 0.


 -4 -1
-4 -1
 D1 =
D1 =  =
= 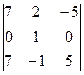 = 1×(-1)4×
= 1×(-1)4× 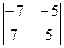 = 0.
= 0.
 |



 D2 =
D2 =  -2 =
-2 = 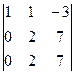 = 1×(-1)2
= 1×(-1)2 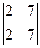 = 0.
= 0.



 D3 =
D3 = 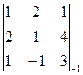 -2 =
-2 = 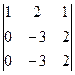 =1×(-1)2×
=1×(-1)2× 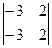 = 0.
= 0.
Так как D = D1 = D2 = D3 = 0, то данная СЛАУ является совместной и неопределенной. Это значит, что в СЛАУ из 3-х уравнений с 3-мя неизвестными, по меньшей мере, одно уравнение представляет собой линейную комбинацию двух других, и, следовательно, эта СЛАУ эквивалентна СЛАУ из 2-х уравнений с 3-мя неизвестными. Поэтому она является неопределенной. Для любой неопределенной СЛАУ, когда число неизвестных превышает ранг основной матрицы (n>r(A)), часть неизвестных называют базисными (главными), а остальные – свободными. Базисными неизвестными называются те, коэффициенты при которых образуют базисный минор. Поскольку базисных миноров может быть несколько, то и вариантов выбора базисных неизвестных также может быть несколько.
В данном примере за базисные неизвестные можно взять любую пару из неизвестных х1, х2, х3, коэффициенты при которых образуют базисный минор. Пусть, например, это будет пара из х1 и х2, так как коэффициенты при них образуют базисный минор в двух первых уравнениях СЛАУ: D/= 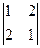 = -3. В данном случае он будет главным определителем новой СЛАУ. Поскольку в определитель D/ вошли только коэффициенты первых двух уравнений, то в новую СЛАУ 3-е уравнение входить не будет, так как оно является линейной комбинацией первых двух уравнений.
= -3. В данном случае он будет главным определителем новой СЛАУ. Поскольку в определитель D/ вошли только коэффициенты первых двух уравнений, то в новую СЛАУ 3-е уравнение входить не будет, так как оно является линейной комбинацией первых двух уравнений.
Оставшаяся неизвестная х3 будет свободной. Зафиксируем ее и чтобы отличить от базисных неизвестных переобозначим: пусть х3 = с3. Теперь в обоих уравнениях новой СЛАУ перенесем с3 в правую часть к свободным членам:
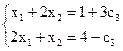
Решим новую СЛАУ по формулам Крамера (4.5).
Главный определитель D/ = -3; первый побочный определитель 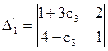 =1+3с3 -2(4-с3)=5с3 -7 Þ х1 =
=1+3с3 -2(4-с3)=5с3 -7 Þ х1 = 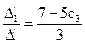 ;
;
второй побочный определитель  = 4-с3-2(1+3с3)=2-7с3 Þ
= 4-с3-2(1+3с3)=2-7с3 Þ
Þ х2 = 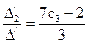 . Ответ: х1 =
. Ответ: х1 =  ; х2 =
; х2 =  ; х3 = с3, где с3 = const.
; х3 = с3, где с3 = const.
Общее решение неопределенной СЛАУ – это множество всех ее частных решений.
Частное решение СЛАУ, получаемое из его общего решения при нулевых значениях свободных неизвестных, называется базисным решением этой СЛАУ. Так, в последнем примере базисным решением СЛАУ будет: х1 = 7/3, х2 = -2/3, х3 = 0.
Дата добавления: 2015-01-09; просмотров: 1278;
