к оформлению студентами индивидуальных домашних работ (ИДР)

1. Вариант ИДР должен соответствовать порядковому номеру фамилии студента в журнале его группы.

2. Каждая ИДР выполняется в отдельной тетради чернилами любого цвета, кроме красного. В тетради должны быть поля для замечаний проверяющего, а в конце тетради должно быть несколько чистых листов для работы над ошибками в соответствии с замечаниями проверяющего.

3. Оформление обложки тетради должно соответствовать образцу:

Индивидуальная домашняя работа

по высшей математике

на тему: Линейная алгебра

студента (ки) гр. ………

Ф.И.О. …………………

вариант № …………….

4. Работа, выполненная по чужому варианту, не засчитывается.

5. Задачи и их решения располагаются в порядке возрастания их номеров в соответствии с нумерацией ИДР.

6. Условие задачи полностью переписывается с заменой общих данных на конкретные из своего варианта.

7. Решение задачи записывается аккуратно и подробно с необходимыми выкладками, чтобы было понятно, откуда что получено.

8. Незачтенная ИДР возвращается студенту для исправления ошибок. Студент должен в конце ИДР в работе над ошибками исправить их и вновь сдать ИДР на проверку.

Список рекомендуемой литературы

1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры.-М.: Наука, 1984. -320с.

2. Ляпин Е.С., Евсеев А.Е. Алгебра и теория чисел. Ч.2. Линейная алгебра и полиномы.-М.: Просвещение, 1978. - 448с.

3. Гурский Е.И. Основы линейной алгебры и аналитической геометрии.-Минск: Вышейш. шк., 1982. - 272с.

4. Гусак А.А. Высшая математика. Т.1.- Минск: ТетраСистемс, 2001. - 544с.

5. Письменный Д.Т. Конспект лекций по высшей математике. 1 часть.-М.: Рольф, 2000. - 288с.

6. Добротин Д.А. Основы линейной алгебры и аналитической геометрии.-Л.: Изд-во Ленингр. ун-та, 1977. - 120 с.

7. Лунгу К.Н. и др. Сборник задач по высшей математике. 1 курс.-М.: Айрис-пресс, 2003. -576с.

Оглавление

Стр.

1. Матрицы…………………………………………………….………………………………….1

1.1. Основные понятия……………………………………….…………………………………..1

1.2. Виды матриц…………………………………………………………………………………1

1.3. Квадратные матрицы………………………………………………………………………..2

1.4. Действия над матрицами……………………………………………………………………3

1.4.1. Линейные действия над матрицами……………………………………………………...3

1.4.2. Умножение матриц………………………………………………………………………..4

1.4.3. Многочлены от квадратных матриц……………………………………………………...6

1.4.4. Транспонирование матриц………………………………………………………………..6

2. Определители………………………………………………………………………………….7

2.1. Понятие определителя………………………………………………………………………7

2.2. Свойства определителей……………………………………………………………………9

3. Невырожденные матрицы…………………………………………………………………...13

3.1. Обратная матрица………………………………………………………………………….13

3.1.1. Вычисление обратной матрицы А^-1 с помощью присоединенной матрицы 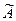…......14

3.1.2. Вычисление обратной матрицы А^-1 методом элементарных преобразований над строками матрицы…….………………………………………………………………………...15

3.2. Ранг матрицы……………………………………………………………………………….16

3.3. Понятие линейной зависимости и линейной независимости..………………………….18

4. Системы линейных алгебраических уравнений (СЛАУ)………………………………….19

4.1. Основные понятия………………………………………………………………………….19

4.2. Матричный способ решения квадратной СЛАУ…………………………………………21

4.3. Формулы Крамера для решения квадратной СЛАУ...…………………………………...22

4.4. Исследование СЛАУ. Теорема Кронекера-Капелли…………………………………….25

4.5. Метод Гаусса исключения неизвестных………………………………………………….26

4.6. Однородная СЛАУ…………………………………………………………………………28

Приложение 1. Индивидуальные задания по теме: «Линейная алгебра»………………..….31

Приложение 2. Образец выполнения индивидуальной домашней работы (ИДР)………….62

Требования к оформлению студентами индивидуальной домашней работы (ИДР)……….68

Список рекомендуемой литературы …………………………………………………………..69