Однородная СЛАУ.
В однородной СЛАУ столбец свободных членов равен нулю. Эта СЛАУ имеет вид
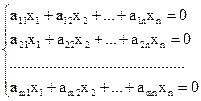 (4.8)
(4.8)
В однородной СЛАУ нулевой столбец не меняется при элементарных преобразованиях над строками расширенной матрицы. Поэтому в ней ранг матрицы коэффициентов всегда равен рангу расширенной матрицы: r(A) = r(A|B). Тогда, по теореме Кронекера-Капелли любая однородная СЛАУ всегда совместна и, согласно ее виду (4.8), всегда имеет нулевое (тривиальное) решение: х1 = … = хn = 0. Если при этом ранг матрицы коэффициентов равен числу неизвестных (r(A) = n), то для однородной СЛАУ нулевое решение является единственно возможным.
Теорема 1.
Для того, чтобы однородная СЛАУ имела ненулевые решения, необходимо и достаточно, чтобы ранг ее матрицы коэффициентов был меньше числа неизвестных (r(A) < n).
Доказательство.
1) Необходимость. Предположим обратное, то есть, что r(A) = n, где n – число неизвестных. Тогда порядок базисного минора Mn будет равен n, так как r(Mn) = r(A) = n. Следовательно, по формулам Крамера однородная СЛАУ будет иметь единственное решение – нулевое: xi =  = 0, где Di = 0, а D ¹ 0. Таким образом, при r(A) = n однородная СЛАУ ненулевых решений не имеет.
= 0, где Di = 0, а D ¹ 0. Таким образом, при r(A) = n однородная СЛАУ ненулевых решений не имеет.
2) Достаточность. Пусть r(A) < n, тогда по следствию 2 теоремы Кронекера-Капелли однородная СЛАУ будет совместной и неопределенной, то есть она будет иметь бесконечное множество решений, в том числе и ненулевых. Fin.
Теорема 2.
Для того, чтобы квадратная однородная СЛАУ имела ненулевые решения, необходимо и достаточно, чтобы ее главный определитель равнялся нулю (D = 0).
Доказательство.
1) Необходимость. По вышеприведенной теореме 1, если однородная СЛАУ имеет ненулевые решения, то ранг ее матрицы коэффициентов должен быть меньше числа неизвестных (r(A) < n). Следовательно, главный определитель квадратной однородной СЛАУ должен быть равен нулю (D = 0).
2) Достаточность. Если главный определитель квадратной однородной СЛАУ равен нулю (D = 0), то ранг ее матрицы коэффициентов будет меньше числа неизвестных (r(A) < n). Поэтому такая СЛАУ имеет бесконечное множество ненулевых решений. Fin.
Пример. Найти ненулевые решения однородной СЛАУ.
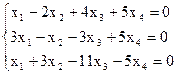
Решение. Запишем расширенную матрицу СЛАУ и элементарными преобразованиями над строками приведем ее к ступенчатому виду.




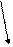

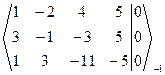 -3 ~
-3 ~ 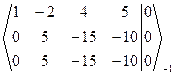 ~
~ 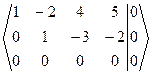 = B
= B
Число неизвестных n = 4 > 2 = r(A) = r(АВ), тогда по теореме 1 однородная СЛАУ помимо нулевого решения имеет и ненулевые решения. Найдем их. Полученной ступенчатой расширенной матрице В соответствует ступенчатая СЛАУ 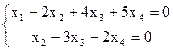
Чтобы решить ее, в качестве базисных можно взять неизвестные х1 и х2, так как коэффициенты при них образуют один из базисных миноров М2 =  = 1 ¹ 0. Следовательно, остальные неизвестные – свободные. Переобозначим их: х3 = с3, х4 = с4 и перенесем в правую часть соответствующих уравнений.
= 1 ¹ 0. Следовательно, остальные неизвестные – свободные. Переобозначим их: х3 = с3, х4 = с4 и перенесем в правую часть соответствующих уравнений.

Ответ: х1 = 2с3-с4; х2 = 3с3+2с4; х3 = с3; х4 = с4, где с3, с4 - const.
Приложение 1.
Индивидуальная домашняя работа (ИДР) по теме:
«Линейная алгебра».
1) Пользуясь свойствами определителей, доказать тождество.
2) Вычислить АТ; А×АТ и ½А½.
3) Решить квадратную СЛАУ:
а) с помощью обратной матрицы;
б) по формулам Крамера.
4) Выполнить действия над матрицами.
5) Найти значения l, для которых существует обратная матрица А-1.
6) Найти ранг r(A) матрицы А.
7(а, б) Исследовать СЛАУ на совместность и решить методом Гаусса.
8) Найти ненулевые решения однородной СЛАУ.
Вариант 1.
1) 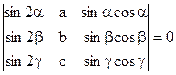
2) А = 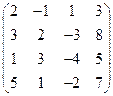
3) 
4) А=  ; В=
; В= 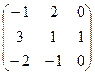 ; А2 - В-1×A=?
; А2 - В-1×A=? 
5) А= 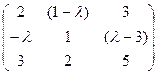
6) А= 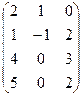 ; r(A)=?
; r(A)=?
7(а) 
7(б) 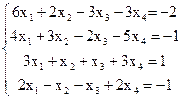
8) 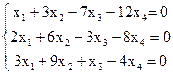
Вариант 2.
1) 
2) А = 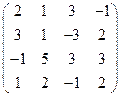
3) 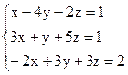
4) А=  ; В=
; В=  ; (А×B)-1 + B×A-1=?
; (А×B)-1 + B×A-1=?
5) А= 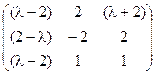
6) А=  ; r(A)=?
; r(A)=?
7(а) 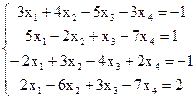
7(б) 
8) 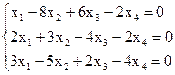
Вариант 3.
1) 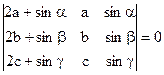
2) А = 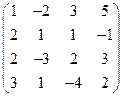
3) 
4) А=  ; В=
; В=  ; А×В-1 + 2B×A=?
; А×В-1 + 2B×A=?
5) А= 
6) А= 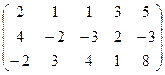 ; r(A)=?
; r(A)=?
7(а) 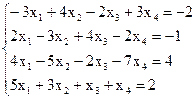
7(б) 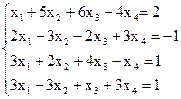
8) 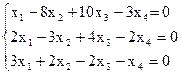
Вариант 4.
1) 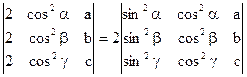
2) А = 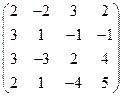
3) 
4) А=  ; В=
; В= 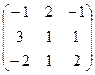 ; А-1×B - A×B-1=?
; А-1×B - A×B-1=?
5) А= 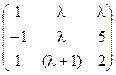
6) А= 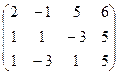 ; r(A)=?
; r(A)=?
7(а) 
7(б) 
8) 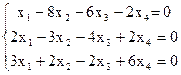
Вариант 5.
1) 
2) А = 
3) 
4) А=  ; В=
; В=  ; А2 - В-1×A=?
; А2 - В-1×A=?
5) А= 
6) А=  ; r(A)=?
; r(A)=?
7(а) 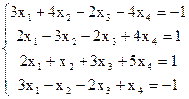
7(б) 
8) 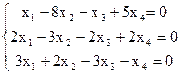
Вариант 6.
1) 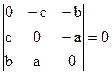
2) А = 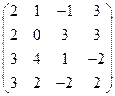
3) 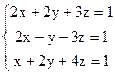
4) А=  ; В=
; В=  ; А2 - В×A-1=?
; А2 - В×A-1=?
5) А= 
6) А= 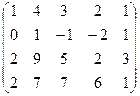 ; r(A)=?
; r(A)=?
7(а) 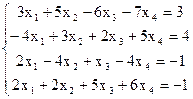
7(б) 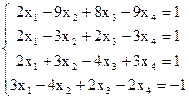
8) 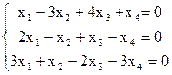
Вариант 7.
1) 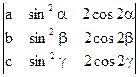 =2
=2 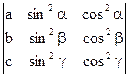
2) А = 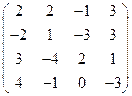
3) 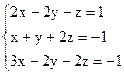
4) А=  ; В=
; В=  ; А×B-1 + В×A=?
; А×B-1 + В×A=?
5) А= 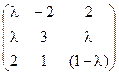
6) А= 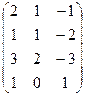 ; r(A)=?
; r(A)=?
7(а) 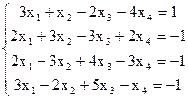
7(б) 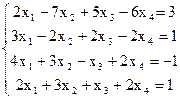
8) 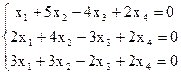
Вариант 8.
1) 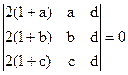
2) А = 
3) 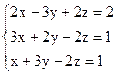
4) А=  ; В=
; В=  ; B×A-1 - A×B-1=?
; B×A-1 - A×B-1=?
5) А= 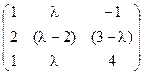
6) А=  ; r(A)=?
; r(A)=?
7(а) 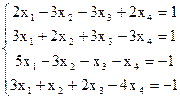
7(б) 
8) 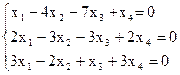
Вариант 9.
1) 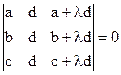
2) А = 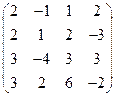
3) 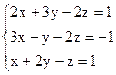
4) А=  ; В=
; В=  ; 2(А×B)-1 - A×В = ?
; 2(А×B)-1 - A×В = ?
5) А= 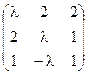
6) А= 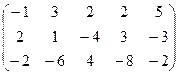 ; r(A)=?
; r(A)=?
7(а) 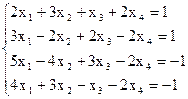
7(б) 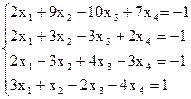
8) 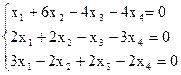
Вариант 10.
1) 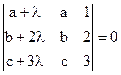
2) А = 
3) 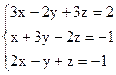
4) А=  ; В=
; В=  ; 2В-1×A + B×A=?
; 2В-1×A + B×A=?
5) А= 
6) А=  ; r(A)=?
; r(A)=?
7(а) 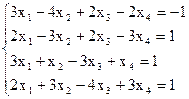
7(б) 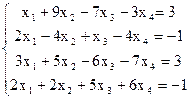
8) 
Вариант 11.
1) 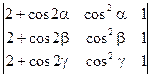 =0
=0
2) А = 
3) 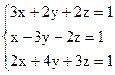
4) А=  ; В=
; В=  ; 2(B×А)-1 + В×A=?
; 2(B×А)-1 + В×A=?
5) А= 
6) А= 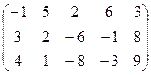 ; r(A)=?
; r(A)=?
7(а) 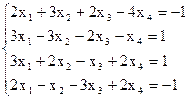
7(б) 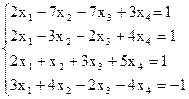
8) 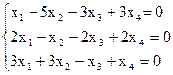
Вариант 12.
1) 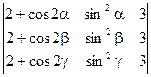 =0
=0
2) А = 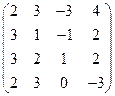
3) 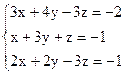
4) А=  ; В=
; В=  ; А×B-1 + 2(B×A)-1=?
; А×B-1 + 2(B×A)-1=?
5) А= 
6) А= 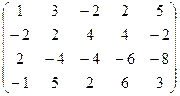 ; r(A)=?
; r(A)=?
7(а) 
7(б) 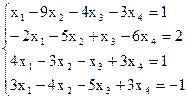
8) 
Вариант 13.
1) 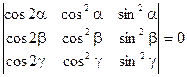
2) А = 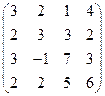
3) 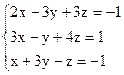
4) А=  ; В=
; В=  ; B-1×А + В×А-1=?
; B-1×А + В×А-1=?
5) А= 
6) А= 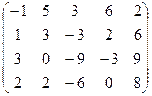 ; r(A)=?
; r(A)=?
7(а) 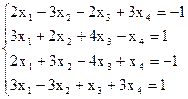
7(б) 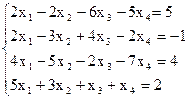
8) 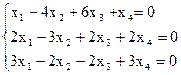
Вариант 14.
1)  =0
=0
2) А = 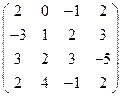
3) 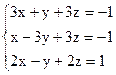
4) А=  ; В=
; В=  ; В×A-1 + B×А=?
; В×A-1 + B×А=?
5) А= 
6) А= 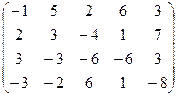 ; r(A)=?
; r(A)=?
7(а) 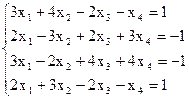
7(б) 
8) 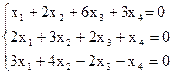
Вариант 15.
1) 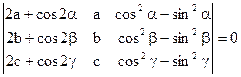
2) А = 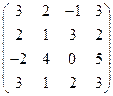
3) 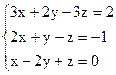
4) А=  ; В=
; В=  ; А-1×B + В-1×А=?
; А-1×B + В-1×А=?
5) А= 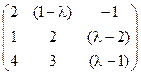
6) А=  ; r(A)=?
; r(A)=?
7(а) 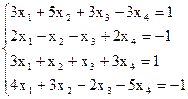
7(б) 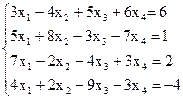
8) 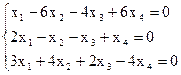
Вариант 16.
1) 
2) А = 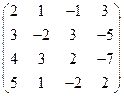
3) 
4) А=  ; В=
; В= 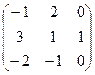 ; А×В - В-1×А-1=?
; А×В - В-1×А-1=? 
5) А= 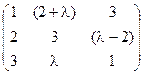
6) А= 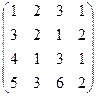 ; r(A)=?
; r(A)=?
7(а) 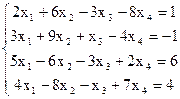
7(б) 
8) 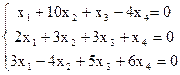
Вариант 17.
1) 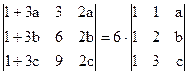
2) А = 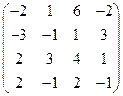
3) 
4) А=  ; В=
; В=  ; (B×A)-1 + A×B-1=?
; (B×A)-1 + A×B-1=?
5) А= 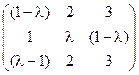
6) А=  ; r(A)=?
; r(A)=?
7(а) 
7(б) 
8) 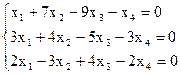
Вариант 18.
1) 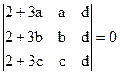
2) А = 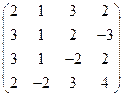
3) 
4) А=  ; В=
; В=  ; В-1×A + 2A×B=?
; В-1×A + 2A×B=?
5) А= 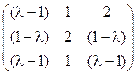
6) А=  ; r(A)=?
; r(A)=?
7(а) 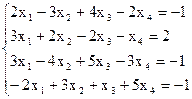
7(б) 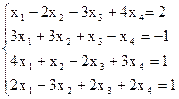
8) 
Вариант 19.
1) 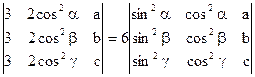
2) А = 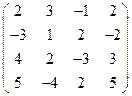
3) 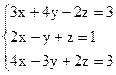
4) А=  ; В=
; В=  ; A-1×B + B×A=?
; A-1×B + B×A=?
5) А= 
6) А= 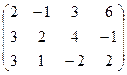 ; r(A)=?
; r(A)=?
7(а) 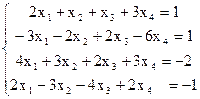
7(б) 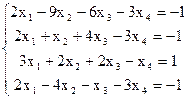
8) 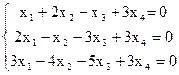
Вариант 20.
1) 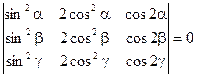
2) А = 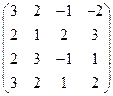
3) 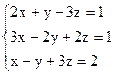
4) А=  ; В=
; В=  ; (А×В)-1 + A×B=?
; (А×В)-1 + A×B=?
5) А= 
6) А= 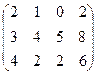 ; r(A)=?
; r(A)=?
7(а) 
7(б) 
8) 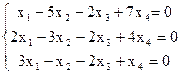
Вариант 21.
1) 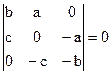
2) А = 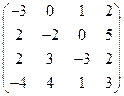
3) 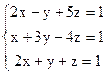
4) А=  ; В=
; В=  ; B×А-1 - В×A=?
; B×А-1 - В×A=?
5) А= 
6) А= 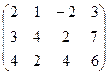 ; r(A)=?
; r(A)=?
7(а) 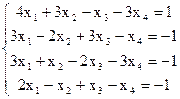
7(б) 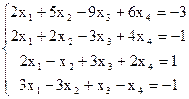
8) 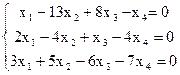
Вариант 22.
1) 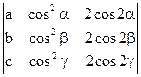 =
= 
2) А = 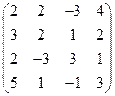
3) 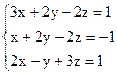
4) А=  ; В=
; В=  ; А×B-1 + (A×B)-1=?
; А×B-1 + (A×B)-1=?
5) А= 
6) А= 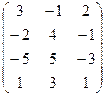
 ; r(A)=?
; r(A)=?
7(а) 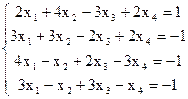
7(б) 
8) 
Вариант 23.
1) 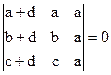
2) А = 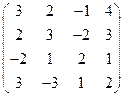
3) 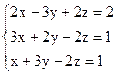
4) А=  ; В=
; В=  ; B×A-1 - A×B-1=?
; B×A-1 - A×B-1=?
5) А= 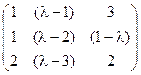
6) А= 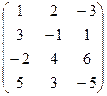 ; r(A)=?
; r(A)=?
7(а) 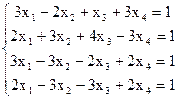
7(б) 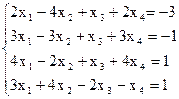
8) 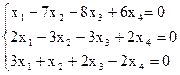
Вариант 24.
1) 
2) А = 
3) 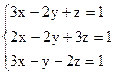
4) А=  ; В=
; В=  ; 2А×B-1 + A-1×В = ?
; 2А×B-1 + A-1×В = ?
5) А= 
6) А= 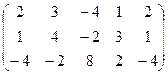 ; r(A)=?
; r(A)=?
7(а) 
7(б) 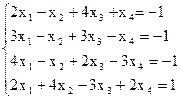
8) 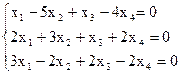
Вариант 25.
1) 
2) А = 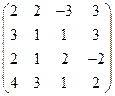
3) 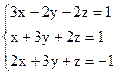
4) А=  ; В=
; В=  ; 2В-1×A + B×A-1=?
; 2В-1×A + B×A-1=?
5) А= 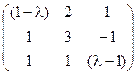
6) А= 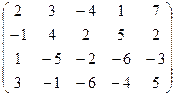 ; r(A)=?
; r(A)=?
7(а) 
7(б) 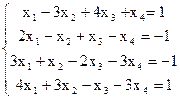
8) 
Вариант 26.
1) 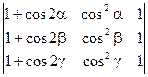 =0
=0
2) А = 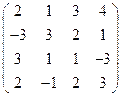
3) 
4) А=  ; В=
; В=  ; (B×А)-1 - 2A×В=?
; (B×А)-1 - 2A×В=?
5) А= 
6) А= 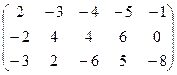 ; r(A)=?
; r(A)=?
7(а) 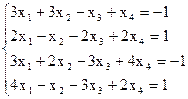
7(б) 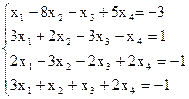
8) 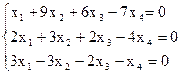
Вариант 27.
1)  =0
=0
2) А = 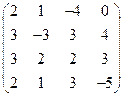
3) 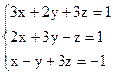
4) А=  ; В=
; В=  ; B-1×A + (A×B)-1=?
; B-1×A + (A×B)-1=?
5) А= 
6) А=  ; r(A)=?
; r(A)=?
7(а) 
7(б) 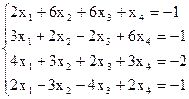
8) 
Вариант 28.
1) 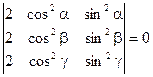
2) А = 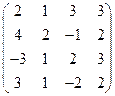
3) 
4) А=  ; В=
; В=  ; А-1×B + A×В-1=?
; А-1×B + A×В-1=?
5) А= 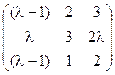
6) А= 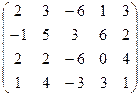 ; r(A)=?
; r(A)=?
7(а) 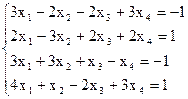
7(б) 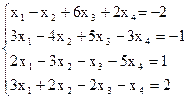
8) 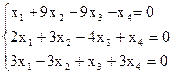
Вариант 29.
1)  =0
=0
2) А = 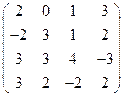
3) 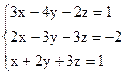
4) А=  ; В=
; В=  ; B-1×A - (B×A)-1=?
; B-1×A - (B×A)-1=?
5) А= 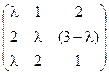
6) А= 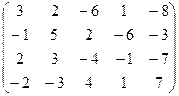 ; r(A)=?
; r(A)=?
7(а) 
7(б) 
8) 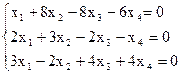
Вариант 30.
1) 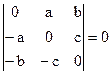
2) А = 
3) 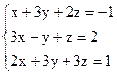
4) А=  ; В=
; В=  ; (B×A)-1 - B×A-1=?
; (B×A)-1 - B×A-1=?
5) А= 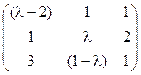
6) А= 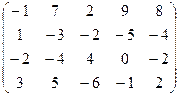 ; r(A)=?
; r(A)=?
7(а) 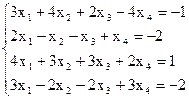
7(б) 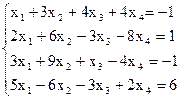
8) 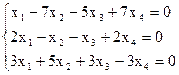
Приложение 2.
Дата добавления: 2015-01-09; просмотров: 1874;
