Методом элементарных преобразований над строками матрицы.

Элементарными преобразованиями матрицы называются:

1) перестановка строк (столбцов) матрицы;

2) умножение элементов строки (столбца) на число l¹0;

3) прибавление элементов одной строки (столбца) к соответствующим элементам другой строки (столбца);

4) вычеркивание нулевой строки (столбца) матрицы.

NB. При элементарных преобразованиях получают только эквивалентные матрицы.

Опр. Матрицы А и В называются эквивалентными (A~B), если одна из них получается из другой в результате конечного числа элементарных преобразований.

Суть метода элементарных преобразований над строками матрицы. К исходной квадратной матрице A_n справа через разделительную вертикальную черту приписывают единичную матрицу Е того же порядка, что и А, и таким образом получают расширенную матрицу (A|E). Далее, с помощью элементарных преобразований над строками приводят матрицу (A|E) сначала к ступенчатому виду (А₁|B), где А₁ – верхняя треугольная матрица, а затем к виду (Е|А^-1). Таким образом, имеет место преобразование: (А|Е)Þ(Е|А^-1).

Пример. Дано: А= 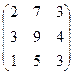. Методом элементарных преобразований над строками найти обратную матрицу А^-1.

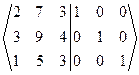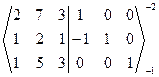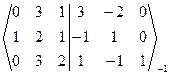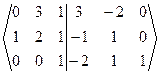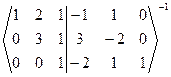Решение. (A|E) = ^-1 ~ ~ ~ ~ ~ ^-1 ~

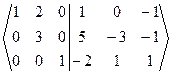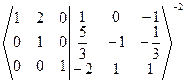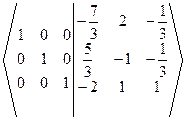~ ~ ~ Þ ÞА^-1=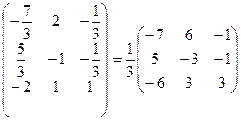

Проверка: А^-1×А = 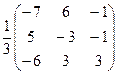× 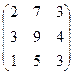= = 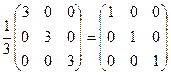Е