Линейные операции над матрицами.

Линейными операциями над матрицами называются:

1) сложение и вычитание матриц;

2) умножение матрицы на действительное число.

Матрицы А и В равны (А = В), если они одинаковой размерности и их соответствующие элементы совпадают, то есть a_ij = b_ij ("i, j).

Опр. 1. Суммой (разностью) матриц А и В одинаковой размерности называется матрица С той же размерности, каждый элемент которой равен сумме (разности) соответствующих (т.е. с одинаковыми индексами) элементов матриц А и В. Тогда для суммы имеем: c_ij=a_ij+b_ij (для разности: c_ij = a_ij – b_ij). Обозначение С = А + В (С = А – В)

Пример. Дано: А = 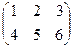, В = . Найти А+В и А-В.

Решение: а) А + В = + = ;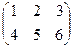

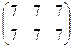б) А – В = - =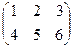

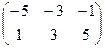
NB. Сложение и вычитание матриц возможно только для матриц одинаковой размерности.

Опр. 2. Произведением матрицы А на действительное число l называется матрица В, получаемая из матрицы А умножением всех ее элементов на числоl: b_ij = l×a_ij . Обозначение В = l×А или В = А×l.

Пример. Дано: А = 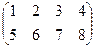, l = -2. Найти l×А.

Решение: l×А = (-2)× =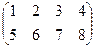

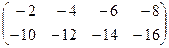
Следствие.

Общий множитель всех элементов матрицы можно выносить за знак матрицы.

Пример. А = 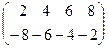= 2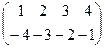

Матрица (-А) = (-1)×А называется противоположной матрице А.

Свойства сложения матриц:

1) коммутативность (переместительное свойство): А + В = В + А;

2) ассоциативность (сочетательное свойство): А + В + С = (А + В) + С = А + (В + С);

3) свойство противоположной матрицы: А + (-А) = О;

4) свойство нулевой матрицы: О + А = А.

Свойства умножения матрицы на число:

5) дистрибутивность (распределительное свойство) относительно суммы матриц:

l×(А+В) = l×А+l×В;

6) дистрибутивность относительно суммы чисел: (l +m)×А = l×А + m×А;

7) ассоциативность (сочетательное свойство) относительно произведения:

l×m×А = (l×m)×А = l×(m×А) = m×(l×А);

8) l×А =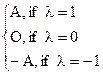

NB 1. Элементы произвольной природы А, В, С …, для которых выполняются линейные операции сложения (Опр. 1) и умножения на число (Опр. 2), и которые удовлетворяют свойствам 1-8, образуют, так называемое, линейное пространство. Примеры линейных пространств: матрицы, векторы, множество действительных чисел R.

NB 2. Для матриц кроме линейных операций имеют место и нелинейные операции - это умножение матрицы на матрицу и операция транспонирования матрицы.

1.4.2. Умножение матрицы на матрицу.

Перемножать можно только согласованные матрицы.

Опр. Матрица А называется согласованной с матрицей В, если число столбцов матрицы А равно числу строк матрицы В. Например, матрица А_m´n является согласованной с матрицей B_n´k, так как в записи их произведении A_m´n× B_n´k внутренние индексы совпадают (n = n). Тогда результирующая матрица С будет иметь размерность внешних индексов: С_m´k. Однако матрица B_n´k не является согласованной с матрицей A_m´n, поскольку в произведении B_n´k× A_m´n внутренние индексы не совпадают (k 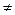m). Следовательно, можно умножить матрицу A_m´n на матрицу B_n´k, но нельзя умножить B_n´k на A_m´n.

Матрицы А и В называются взаимно согласованными, если А согласована с В, а В согласована с А. Это бывает, если А и В – квадратные матрицы одного порядка или если A_m´n, а B_n´m.

NB. Умножение матрицы А на матрицу В обозначается символом А×В. Произведение матриц А×В еще называют умножением слева матрицы А на матрицу В либо умножением справа матрицы В на матрицу А.

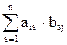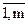Опр. Произведением матрицы A_m´n на матрицу B_n´k называется матрица C_m´k, каждый элемент которой c_ij = a_i1b_1j + a_i2b_2j + … + a_inb_nj = (i = ; j = 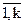), то есть элемент c_ij равен сумме попарных произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В. Или кратко: элемент c_ij равен произведению i-ой строки матрицы А на j-тый столбец матрицы В.

На рисунке 1.4 схематично показан пример получения элемента с₂₁ матрицы С.

A_4x3 B_3x5 C_4x5

. =

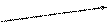
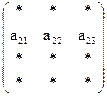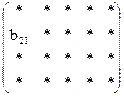
с₂₁ = а₂₁×b₁₁ + а₂₂×b₂₁ + а₂₃×b₃₁

Рисунок 1.4

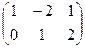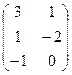Пример. Дано: А= ; В= . Найти А×В и В×А.

Решение. Так как матрицы А и В взаимно согласованы, то получим

1) А_2×3 ×В_3×2 = С_2×2;

А_2х3×В_3х2= . = = = ;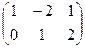

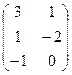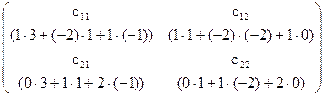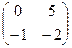2) В_3×2 ×А_2×3 = D_3×3;

2) В_3х2×А_2х3= . = = =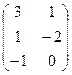

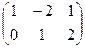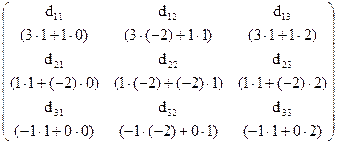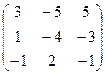
NB. Очевидно, что в общем случае, произведение двух матриц не обладает переместительным свойством, то есть А×В 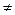В×А.

Матрицы А и В называются коммутативными (перестановочными), если А×В = В×А.

NB. Матрицы Е и О всегда являются перестановочными по отношению к другим матрицам, так как

1) А×Е = Е×А = А

2) А×О = О×А = О

Свойства умножения матриц:

1) А×В 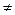В×А;

2) (А×В)×С=А×(В×С) – ассоциативность (сочетательное свойство);

3) А×(В+С)=А×В+А×С или (А+В)×С=А×С+В×С – дистрибутивность (распределительное свойство);

4) l×(А×В)=(l×А)×В=А×(l×В), где l - заданное число.

NB. Формально в линейной алгебре не определяется операция деления матрицы А на матрицу В, однако фактически она реализуется умножением матрицы А на, так называемую, обратную матрицу В^-1, нахождение которой будет рассмотрено ниже.

1.4.3. Многочлены от квадратных матриц.

Опр. Квадратная матрица А в n–ой степени есть произведение матрицы А на себя n раз: Аⁿ = (nÎN). Квадратная матрица А (А¹О) в нулевой степени есть единичная матрица Е того же порядка, что и матрица А, то есть А⁰ = Е.

NB. Возводить в степень можно только квадратные матрицы.

Свойства степени квадратной матрицы:

1) А^m×Aⁿ = A^m+n

2) (A^m)ⁿ = A^m×n

Из обычного многочлена (полинома) степени n (nÎZ₊)

P_n(x)=a_n×xⁿ + a_n-1×x^n-1 + …+ a₁×x¹ + a₀×x⁰

заменой переменной х на квадратную матрицу А получают матричный многочлен Р_n(А) от квадратной матрицы А: P_n(A) = a_n×Aⁿ + a_n-1×A^n-1 + …+ a₁×A + a₀×Е, который также является матрицей.

NB. В матричных многочленах от квадратной матрицы А порядок единичной матрицы Е равен порядку матрицы А.

Пример. Найти значение функции f(x) при х=А, если f(x)=x²-2x+2, A= .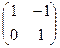

Решение: так как единичная матрица Е в матричном исчислении играет роль единицы, то искомое значение функции следует искать в виде

f(A) = A²-2A+2E = =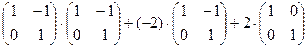

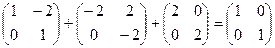= = Е

Опр. Матрица А называется корнем многочлена Р_n(х), если Р_n(А)=0. В этом случае многочлен Р_n(х) называется аннулирующим многочленом для матрицы А.

Пример. Показать, что матрица А= 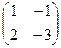является корнем многочлена Р₂(х) = х² + 2х -1.

Решение: Р₂(А) = А² + 2А - Е =

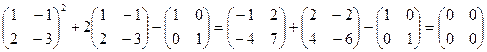= = О