Квадратные матрицы.
Элементы с одинаковыми индексами a11, а22, …, ann образуют главную диагональ квадратной матрицы. Поэтому эти элементы называются диагональными элементами. Геометрически главная диагональ проходит через левый верхний и правый нижний угол квадратной матрицы (рис.1.2).
Рисунок 1.2
Соответственно побочная диагональ квадратной матрицы проходит через ее правый верхний и левый нижний угол (рис.1.3).


Рисунок 1.3
Диагональная матрица – это квадратная матрица, у которой все элементы, лежащие вне главной диагонали равны нулю.
A = 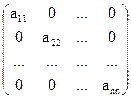
NB. В диагональной матрице среди ее диагональных элементов могут быть и нули, но только не на концах главной диагонали, т.е. а11¹0, аnn¹0.
Частным случаем диагональной матрицы является единичная матрица. Единичная матрица - это диагональная матрица, у которой все диагональные элементы равны единице. Она обозначается буквой Е.
E = 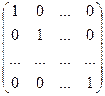
Ее краткое обозначение E = 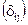 , где dij – это символ Кронекера,
, где dij – это символ Кронекера, 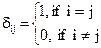
NB. В матричном исчислении единичная матрица играет ту же роль, что и число 1 в арифметике.
Треугольная матрица – это квадратная матрица, у которой все элементы, расположенные выше (или ниже) главной диагонали, равны нулю. В верхней треугольной матрице равны нулю все элементы, расположенные ниже главной диагонали. В нижней треугольной матрице равны нулю все элементы, расположенные выше главной диагонали.
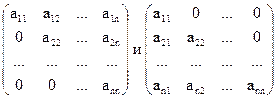
Дата добавления: 2015-01-09; просмотров: 1308;
