Матрицы
Круговая диаграмма может быть построена и для плоского напряженного состояния, заданного исходными напряжениями 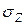 ,
, 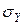 ,
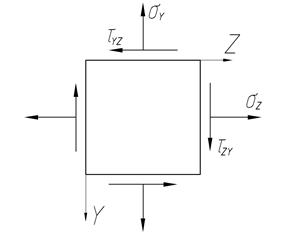
, 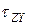 .
.
Порядок геометрического анализа следующий.
1. Вычерчивается прямоугольная система координат 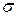 и
и 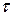 .
.
2. Наносится точки с координатами ( 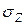 ,
, 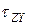 ) и (
) и ( 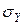 ,
, 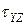 ). Эти точки соответствуют своим площадкам.
). Эти точки соответствуют своим площадкам.
3. Полученные точки соединяются прямой линией и отмечается пересечение этой линии с осью 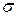 – центр круга Мора.
– центр круга Мора.
4. Пересечение круга Мора с осью 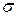 дает значения главных напряжений.
дает значения главных напряжений.
5. Пересечение исходных площадок с кругом Мора дает полюс, из которого можно определить положение любой неизвестной площадки.
На круге Мора можно также определить значения напряжений на площадках под заданным углом 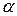
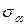 и
и 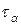 .
.
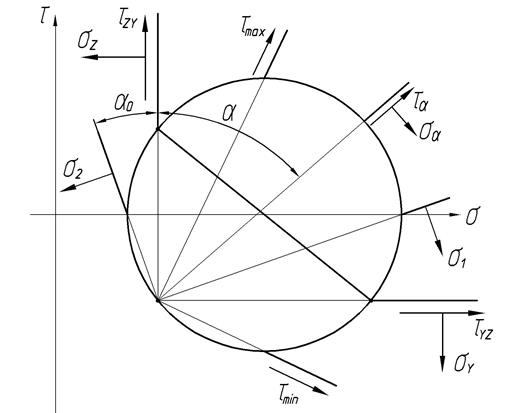
Из круга Мора можно определить экстремальные значения касательных напряжений
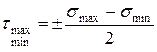 .
.
Следует заметить, что площадки, по которым действуют экстремальные касательные напряжения, повернуты относительно главных площадок на 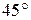 .
.
19)Обобщ. з, Гука при объемн. деф. Объемн. деформация.
Матрицы
Основные понятия.
Опр. Числовая матрица размерности m´n – это прямоугольная таблица чисел, состоящая из m строк и n столбцов. Строки матрицы – это горизонтальные ряды чисел, столбцы матрицы – это вертикальные ряды чисел. Числа матрицы называются элементами матрицы. Матрицы обычно заключены в круглые скобки.
Обозначаются матрицы заглавными буквами латинского алфавита, а их элементы - соответствующими малыми буквами с двумя индексами. Например, для матрицы А, ее элементы обозначаются символами аij, где первый индекс i указывает номер строки, а второй индекс j – номер столбца данного элемента (i = 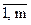 ; j =
; j = 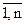 ) (рис.1.1).
) (рис.1.1).

 j
j

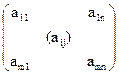
i
Рисунок 1.1
Матрица А размерности m´n кратко обозначается символом Am´n и имеет вид
Am´n = 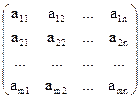
Дата добавления: 2015-01-09; просмотров: 898;
