Транспонирование матриц.

Опр. Если в матрице А поменять местами строки на столбцы с сохранением их нумерации, то получится транспонированная матрица А^т.

Пример. Дано: А= 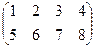. Найти: 1) А^т, 2) А∙ А^т

А_2×4 С_2×2

Решение: 1) А^т = 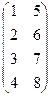; 2) А∙ А^т = ∙ =

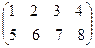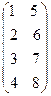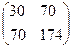
Свойства операции транспонирования:

1) (А^т)^т=А;

2) (А+В)^т=А^т+В^т;

3) (l×А)^т=l×А^т;

4) (А×В)^т=В^т×А^т.

NB. Транспонирование квадратной матрицы сводится к повороту ее элементов вокруг главной диагонали на угол p.

Опр. Симметрические матрицы – это квадратные матрицы, у которых равны элементы, симметричные относительно главной диагонали, то есть a_ij = a_ji.