Предел функции

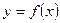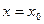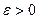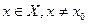Число А называется пределом функции в точке , если для любого существует такое, что для всех , удовлетворяющих неравенству 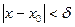, выполняется неравенство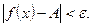

Записывают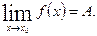

Функция 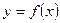называется непрерывной в точке 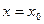, если предел функции и ее значение в этой точке равны,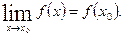

Первый замечательный предел .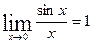

Второй замечательный предел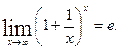

Правило Лопиталя: если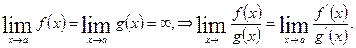

Пример1. Найти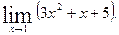

Решение.

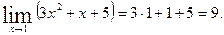
Пример2. Вычислить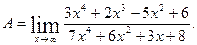

Решение.

Заменяя каждый из многочленов своим старшим членом, имеем: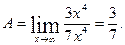

Пример3. Найти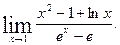

Решение.

Имеем неопределенность вида 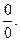Применяя правило Лопиталя, получаем

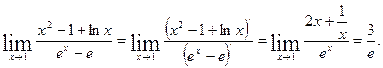
Пример4. .Вычислить предел

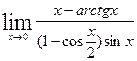
Решение.

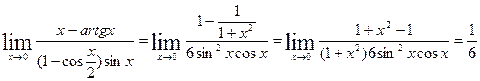Ответ:

Пример5. Найти асимптоты функции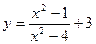

Решение.

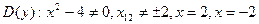-вертикальные асимптоты.

,

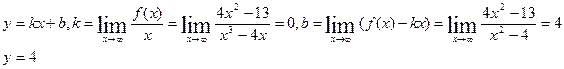Ответ: 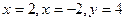-асимптоты.