Интеграл
Определение Функция 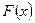 назывется первообразной функции
назывется первообразной функции 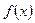
, если ее производная равна 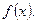
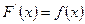 .
.
Определение.Если 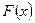 - некая первообразная для функции
- некая первообразная для функции 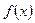 , то
, то 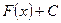 , где С – некая постоянная, дает нам совокупность всех первообразных функции
, где С – некая постоянная, дает нам совокупность всех первообразных функции 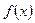 и называется неопределенным интегралом функции
и называется неопределенным интегралом функции 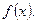
Обозначение его 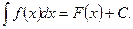
Основные свойства неопределенного интеграла:
1. 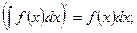
2. 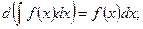
3. 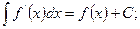
4. 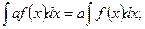
5. 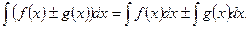
Таблица основных интегралов:
1. 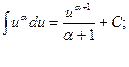 7.
7. 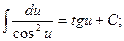
2. 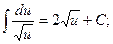 8.
8. 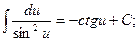
3. 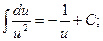 9.
9. 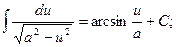
4. 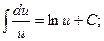 10.
10. 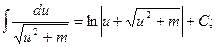
5. 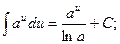 11.
11. 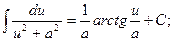
6. 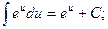 12.
12. 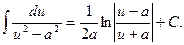
Формула интегрирования по частям 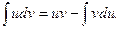
Определение. Пусть на замкнутом промежутке 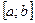 задана непрерывная функция
задана непрерывная функция 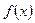 и
и 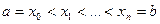 - произвольное разбиение отрезка
- произвольное разбиение отрезка 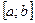 .
.
Сумма вида 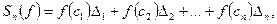 где
где 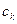 - некоторое число из отрезка
- некоторое число из отрезка 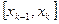 , а
, а 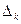 - длина этого отрезка, называется интегральной суммой функции
- длина этого отрезка, называется интегральной суммой функции 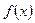 на отрезке
на отрезке 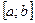 .
.
Определенным интнгралом от функции 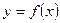 на отрезке
на отрезке 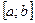 называется предел последовательности интегральных сумм при бесконечном дроблении отрезка
называется предел последовательности интегральных сумм при бесконечном дроблении отрезка 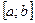 , обозначают
, обозначают 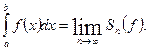
Формула Ньютона-Лейбница: 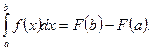
Пример 1. Вычислить интеграл 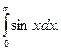
Решение. 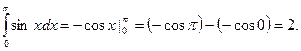
Пример 2. Найти неопределенный интеграл
1) 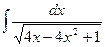
Решение.
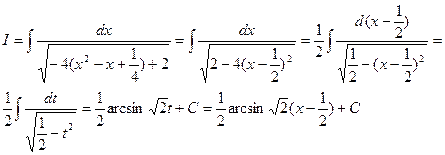
 Ответ:
Ответ: 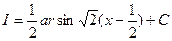
2) 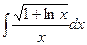
Решение.
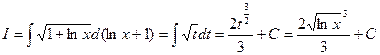
Ответ: 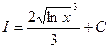
3) 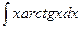
Решение.
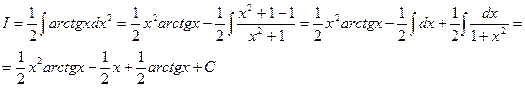
Ответ: 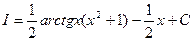
Пример 3. Вычислить 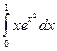
Решение.
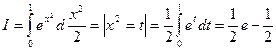

Ответ: 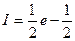
Пример 4. Определить объем тела вращения вокруг оси абсцисс плоской фигуры, ограниченной кривыми 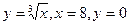
Решение.
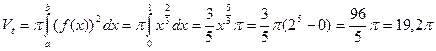
Ответ: 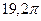
Дата добавления: 2015-01-09; просмотров: 1239;
