Основные характеристики выборки
Статистика – это наука, изучающая, обрабатывающая и анализирующая количественные данные о разнообразнейших массовых явлений в жизни.
Экономическая статистика изучает изменение цен, спроса и предложения товаров, прогнозирует рост и падение производства и потребления.
Математическая статистика – это раздел математики, изучающий математические методы обработки и использования статистических данных для научных и практических выводов.
Генеральная совокупность – это вся совокупность однородных объектов, которую изучают относительно некоторого признака, который характеризует эти объекты.
Выборкой называют совокупность случайно выбранных объектов из генеральной выборки.
Статистическим распределением называют перечисление вариант и соответствующих им частот.
Эмпирической функцией распределения называют функцию 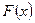 , которая определяет для каждого х относительную частоту
, которая определяет для каждого х относительную частоту 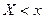 , то есть
, то есть  где
где 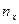 - число вариант меньших х,
- число вариант меньших х, 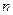 - объем выборки.
- объем выборки.
Основные числовые характеристики выборки:
Медиана – это так называемое среднее значение упорядоченного ряда значений случайной величины: 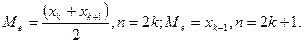
Мода – это вариант, который имеет большую частоту, встречается чаще других.
Размах выборки – это разность между наибольшим и наименьшим значениями случайной величины выборки.
Среднее выборочное - 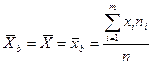
Дисперсия - 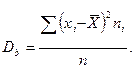
Среднее квадратичное отклонение - 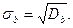
Коэффициент вариации - 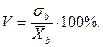
Подобно тому, как графики всех парабол можно получить с помощью геометрических преобразований одной параболы 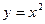 , так и все кривые нормальных распределений можно получить с помощью геометрических преобразований одной кривой. Эту кривую называют кривой нормального распределения, или гауссовой кривой:
, так и все кривые нормальных распределений можно получить с помощью геометрических преобразований одной кривой. Эту кривую называют кривой нормального распределения, или гауссовой кривой:  .
.
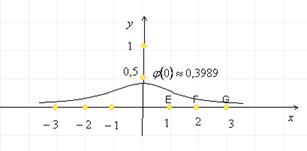
Правило трех сигм:
68% (или приблизительно 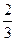 ) всех значений нормального распределения случайной величины Х имеют отклонение от среднего значения, по абсолютной величине не превышающее среднее квадратичное отклонение
) всех значений нормального распределения случайной величины Х имеют отклонение от среднего значения, по абсолютной величине не превышающее среднее квадратичное отклонение 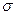 , а 96% всех значений – не превышающее
, а 96% всех значений – не превышающее  . Почти все значения (точнее, 99,7 всех значений) имеют отклонение от среднего, не превышающего по абсолютной величине утроенное среднее квадратичное отклонение
. Почти все значения (точнее, 99,7 всех значений) имеют отклонение от среднего, не превышающего по абсолютной величине утроенное среднее квадратичное отклонение 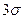 .
.
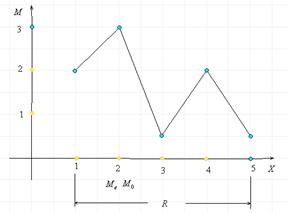
Пример 1.Найдите размах, моду, медиану и среднее значение ряда данных некоторой случайной величины 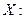 1, 1, 2, 2, 2, 3, 4, 4, 5. Постройте полигон частот значений случайной величины
1, 1, 2, 2, 2, 3, 4, 4, 5. Постройте полигон частот значений случайной величины 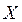 . Укажите на рисунке размах, моду, медиану заданного ряда данных.
. Укажите на рисунке размах, моду, медиану заданного ряда данных.
Решение.
Размах выборки: 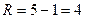 .
.
Среднее значение: 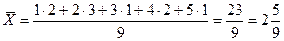 .
.
Мода выборки: 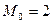 , так как число 2 повторяется чаще всего.
, так как число 2 повторяется чаще всего.
Медиана: 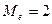 , так как именно это число стоит в центре ряда.
, так как именно это число стоит в центре ряда.
Постоим полигон частот.
Пример 2.Выигрыши (в грн.), которые приходятся на один билет в каждой их двух лотерей, имеют следующие законы распределения:
1)
| Х | ||||
| Р | 0,9 | 0,06 | 0,03 | 0,01 |
2)
| Х | ||||
| Р | 0,85 | 0,12 | 0,02 | 0,01 |
Какой из этих лотерей вы отдадите предпочтение?
Решение.
Найдем математическое ожидание каждого распределения.
1) 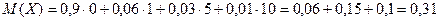 .
.
2) 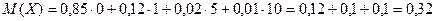 .
.
Сравним два числа и получим, что вторая выгодней.
Пример 3. Задана генеральная совокупность из 20 элементов. Выполнить задания:
1) построить статистическое распределение и ее эмпирическую функцию распределения;
2) вычислить ее числовые характеристики выборки: среднее, дисперсию и среднее квадратичное отклонению
Решение.
Дана генеральная выборка:
15,19,13,12,9,14,15,19,12,17,13,9,15,12,15,14,18,16,15,12.
1) Статистическое распределение выборки имеет вид:

| |||||||||
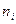
|
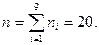
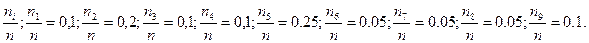
Эмпирическая функция распределения имеет вид:
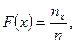 где
где 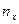 - число вариантов, меньших чем х;
- число вариантов, меньших чем х; 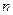 - объем выборки;
- объем выборки; 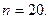 Тогда имеем:
Тогда имеем:
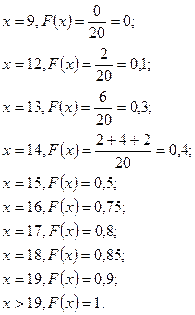 или
или 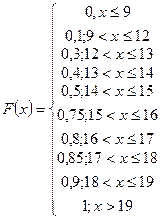
2) Числовые характеристики выборки:
Среднее 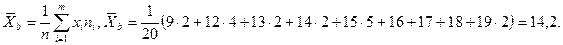
Выборочная дисперсия 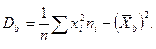
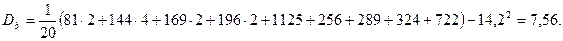
Среднее квадратичное отклонение 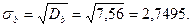
ВОПРОСЫ К ЭКЗАМЕНУ
1. Натуральные числа. Действия с натуральными числами. Метод математической индукции
2. Целые числа, правила сложения, умножения и деления с целыми числами
3. Дробные числа. Обыкновенные и десятичные дроби. Действия над ними.
4. Квадратные корни. Свойства квадратного корня
5. Действительные числа. Десятичная запись действительного числа. Действия на множестве действительных чисел.
6. Числовая прямая. Модуль числа.
7. Проценты. Задачи на проценты.
8. Пропорция, основное свойство пропорции.
9. Функция, определение и способы задания.
10. Свойства элементарных функций.
11. Графики элементарных функций.
12. Предел функции.
13. Производная функции, таблица производных.
14. Первообразная для функции.
15. Определённый интеграл.
16. Таблица интегралов. Формула Ньютона-Лейбница.
17. Комбинаторика. Перестановки, сочетания и размещения.
18. Бином Ньютона.
19. Вариационный ряд. Размах, мода и медиана ряда.
20. Статистическое распределение. Полигон.
21. Среднее ряда.
22. Дисперсия и среднее квадратичное отклонение.
Примерный вариант контрольной работы
1. Найти значение выражения 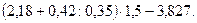
2. Вкладчик положил в банк 40 000 грн. под 8% простых годовых. Сколько денег будет на его счёте через 3 года?
3. Построить график 
4. Используя правила и формулы дифференцирования найти производные функций: 1) 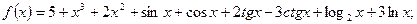
2) 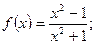 3)
3) 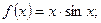 4)
4) 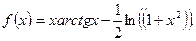
5. Вычислить интеграл 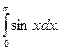
6. Найти разложение: 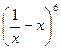
7. Сколько трехзначных чисел можно составить из цифр 1,2,3,4, если цифры не повторяются?
8. Группа студентов из 12 человек сдают экзамен по математике. Знания оценивались по пятибалльной системе. Оценки, полученные студентами соответствующие списку, такие: 5,4,4,3,4,2,2,5,5,3,3,4. Найти медиану этого распределения.
ЛИТЕРАТУРА
Учебники:
1. Шкіль М.І., Колесник Т.В., Котлова В.М. Математика для економістів: Аналітична геометрія з елементами алгебри. Вступ до математичного аналізу- К.: Либідь,1994
2. Шкіль М.І., Колесник Т.В. Математика для економістів: диференціальне та інтегральне числення функції однієї змінної, ряди. - К.: Либідь,1994.
3. Шкіль М.І., Колесник Т.В. Математика для економістів: диференціальне та інтегральне числення функцій багатьох змінних, диференціальні рівняння. - К.: Либідь,1994.
4. Жильцов О.Б. Математика для економістів з елементами інформаційних технологій. – К.: МАУП, 2002.
5. Шнейдер В.Е. Краткий курс высшей математики. Т 1 – М.: Высш. шк., 1978.
6. Шнейдер В.Е. Краткий курс высшей математики. Т 2 – М.: Высш. шк., 1980.
7. Яковлев Г.Н. Высшая математика. – М.: Просвещение, 1988.
8. Колесников А.Н. Краткий курс высшей математики для экономистов. Учебное пособие.- М.: ИНФРА-М, 2001.-208с.
9. Лебедев В.В. высшая математика для менеджера. -М.: ЗАО»Финстатинформ»,1999.-137с.
Задачники:
10. Минорский В.П. Сборник задач по высшей математике.- М.: Наука,1987
11. Демидович Б.П., Ефимов А.В. Сборник задач по математике для ВТУЗОВ. Часть 1.- М.: Наука, 1981
12. Демидович Б.П., Ефимов А.В. Сборник задач по математике для ВТУЗОВ. Часть 2.- М.: Наука, 1981
13. Тевяшев А.Д., Литвин А.Г. Сборник задач и упражнений по высшей математике.-Харьков: ХТУР,2000.
Дата добавления: 2015-01-09; просмотров: 3347;
