Предельная погрешность
Из предыдущего рассмотрения свойств случайных погрешностей следует, что о появлении отдельной погрешности заранее что–либо определенное сказать невозможно. Однако, когда число этих погрешностей возрастает, можно установить определенные закономерности для всей совокупности погрешностей данного ряда измерений. Эти закономерности можно выразить уравнением, полученным К. Ф. Гауссом. Оно имеет вид
__ 2 2 __ 2 2
y = (1 / σ √2π ) e – (li – a) / 2σ = (1 /σ √2π ) e – Δc / 2σ , (4.17)
где y – плотность распределения погрешностей;
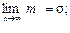 σ – параметр уравнения, называемый стандартом, связан со средней
σ – параметр уравнения, называемый стандартом, связан со средней
квадратической погрешностью соотношением
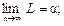 a – параметр уравнения, называемый математическим ожиданием,
a – параметр уравнения, называемый математическим ожиданием,
связан с арифметической срединой соотношением
e – основание натуральных логарифмов;
Δi = li – a – случайная погрешность.
Это уравнение называется законом нормального распределения погрешностей.
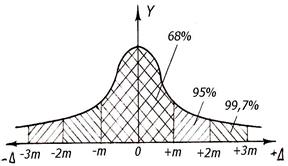 |
Уравнению (4.17) соответствует колоколообразная кривая, называемая кривой нормального распределения (кривая Гаусса) (рисунок 4.1)
Рисунок 4.1 – Кривая Гаусса
Площадь под кривой, ограниченная кривой и осью абсцисс, принимают равной единице. Часть этой площади, соответствующая какому-либо отрезку оси абсцисс, дает, вероятность попадания случайной погрешности в данный интервал. При li = a или Δ = 0 получаем максимальное значение ординаты кривой __
Y = 1 / σ √2π.
Из рисунка 4.1 видно, что основная масса погрешностей группируется около наиболее вероятного значения погрешности Δi = 0 (согласно четвертому свойству случайных погрешностей, среднее арифметическое из случайных погрешностей стремится к нулю). Это положение обосновывает третье свойство случайных погрешностей (малые погрешности встречаются чаще, чем большие). Второе свойство случайных погрешностей о равном появлении положительных и отрицательных ошибок характеризуется симметричностью кривой нормального распределения относительно оси OY.
Теоретические исследования и практика геодезических измерений показывают, что в промежутках от –m до +m попадает 68 % всех случайных погрешностей (см. рисунок 4.1), в промежуток вдвое больший (от –2m до +2m) попадает 95 % погрешностей, а в промежуток втрое больший (от –3m до +3m) попадает 99,73 % погрешностей. Это означает, что из 100 погрешностей измерений только 32 по абсолютной величине превзойдут среднюю квадратическую погрешность m, 3 из 1000 погрешностей будет превышать величину утроенной средней квадратической погрешности ±3m. Таким образом, за пределы ±3m выходит лишь 0,27 % погрешностей измерений. Поэтому в качестве предельной погрешности Δпред принимается утроенная средняя квадратическая погрешность, т. е.
Δпред = 3m. (4.18)
Рассмотрим теперь сущность параметров a и σ в уравнении (4.17). Параметр a называемый математическим ожиданием и характеризует центр группирования на кривой Гаусса, т. е. смещение центра группирования вдоль оси абсцисс (рисунок 4.2, а) при сохранении формы кривой. Если при постоянном значении параметра a будем изменять другой параметр σ (называемый стандартом), характеризующий точность измерений, а это возможно, если мы меняем метод измерений или выполняем их другими приборами. Тогда центр группирования остается неизменным, а форма кривой изменится. Она станет более пологой, если точность измерений уменьшается, и станет более крутой при увеличении точности (рисунок 4.2, б).
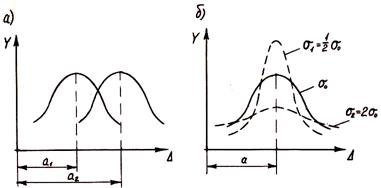 |
Рисунок 4.2 – Смещение и изменение формы нормальной кривой
Параметры a и σ заранее, до измерений, неизвестны. Они получаются как результат большого числа измерений. На практике вместо параметров a и σ мы получаем приближенные их значения: арифметическую средину L, вычисляемую по формуле (4.4), и среднюю квадратическую погрешность m, вычисляемую по формулам (4.5) или (4.15).
Дата добавления: 2015-01-19; просмотров: 1944;
