Функция общего вида

φ = f (X, Y, Z, … ,U), (4.37)

где X, Y, Z, … ,U – независимо измеренные величины.

С учетом случайных погрешностей функция (4.37) примет вид

φ + Δ_φ = f (X + Δ_X; Y + Δ_Y ; Z + Δ_Z ; …; U + Δ_U). (4.38)

Разложив функцию (4.38) в ряд Тейлора и ограничившись только первыми степенями случайных погрешностей, получим функцию

Δ_φ = (∂f/∂x) Δ_X + (∂f/∂y) Δ_Y + (∂f/∂z) Δ_Z + … + (∂f/∂u) Δ_U, (4.39)

где (∂f/∂x), (∂f/∂y), …, (∂f/∂u) – частные производные, которые для функции

(4.39) являются постоянными величинами.

Как видно, функция (4.39) аналогична функции (4.33). Следовательно, квадрат ее средней квадратической погрешности

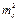
= (∂f/∂x ∙ m_X)² + (∂f/∂y ∙ m_Y)² + (∂f/∂z ∙ m_Z)² + … + (∂f/∂u ∙ m_U)². (4.40)

П р и м е р. В прямоугольнике измерены две стороны – Х = 200 м и Y = 100 м со средними квадратическими погрешностями m_X = +0,20 м и m_Y = +0,10 м.

Определить площадь прямоугольника Р и ее среднюю квадратическую погрешность m_P.

P = XY; ∂p/∂x = Y; ∂p/∂y = X ;

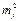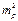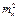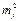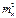= (∂p/∂x)² + (∂p/∂y)² = Y ² + X² =

____ = 100² ∙ 0,20² + 200² ∙ 0,10² = 800 м²;

M_p = √ 800 ≈ ±28 м²; Р = 200 × 100 = 20000 м² ± 28 м².