Функция линейного вида

φ = КХ,

где К – постоянное число;

Х – аргумент, полученный из измерений.

Если Х будет измерен со случайной погрешностью Δ_Х, то функция будет иметь случайную погрешность

Δ_φ = К Δ_X. (4.29)

Измерив аргумент n раз, можно составить n уравнений (4.29), взять сумму их квадратов и разделить на n. После чего получим

[Δ 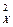] / n = K² [Δ 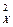] / n или m 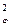= K² m 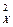, (4.30)

откуда

m_φ = K m_X . (4.31)

Аналогично предыдущему можно показать, что для функции

φ = ± K₁X ± K₂Y ± … ± K_nU (4.32)

получим

Δ_φ = K₁Δ_X ± K₂Δ_Y ± … ± K_nΔ_U (4.33)

или

m 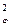= (K₁m_X)² + (K₂m_Y)² + … + (K_nm_U)². (4.34)

П р и м е р. Определить среднюю квадратическую погрешность M арифметической середины L, если средняя квадратическая погрешность отдельного измерения равна m. Напишем формулу (4.4) арифметической середины в следующем виде:

L = l₁ / n + l₂ / n + … + l_n / n. (4.35)

Как видно, здесь можно применить формулу (4.34) для функции (4.35):

m 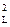= M ² = (m₁ / n)² + (m₂ / n)² + … + (m_n / n)².

Учитывая, что измерения l₁, l₂,…, l_n равноточные, т. е. m₁ = m₂ = … = m_n, получим

M ² = n(m / n)² = m² / n,

или __

M = m / √n , (4.36)

т. е. средняя квадратическая погрешность арифметической средины в √n раз меньше средней квадратической погрешности отдельного измерения.