Функция суммы двух аргументов
φ = Х + Y, (4.19)
где Х и Y – независимо измеренные величины.
Допустим, что каждая из этих величин измерялась n раз и каждое из измерений сопровождалось случайными погрешностями ΔХ и ΔY. Тогда и функция φ, вычисленная по формуле (4.19), будет иметь погрешность Δφ:
φ + Δφ = (X + ΔX) + (Y + ΔY) или Δφ = ΔХ + ΔY. (4.20)
Возведем равенство (4.20) в квадрат:
Δ 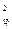 = Δ
= Δ 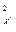 + Δ
+ Δ 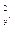 + 2ΔX ΔY. (4.21)
+ 2ΔX ΔY. (4.21)
Таких равенств может быть получено n. Сложив их и разделив на n, получим
[Δ 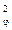 ] / n = [Δ
] / n = [Δ 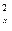 ] / n + [Δ
] / n + [Δ 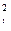 ] / n + 2[ΔXΔY] / n. (4.22)
] / n + 2[ΔXΔY] / n. (4.22)
На основании четвертого свойства случайных погрешностей величина [ΔX ΔY] как сумма случайных погрешностей будет стремиться к нулю. Тогда с учетом равенства (4.5) будем иметь:
m 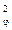 = m
= m 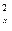 + m
+ m 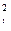 . (4.23)
. (4.23)
Нетрудно убедиться, что формула (4.23) будет верна и для функции
φ = X –Y. (4.24)
Аналогично предыдущему можно доказать, что для функции суммы (разности) нескольких аргументов
φ = ±Х ± Y ± Z ± … ± U. (4.25)
Квадрат средней квадратической погрешности этой функции будет равен сумме квадратов средних квадратических погрешностей аргументов:
m 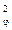 = m
= m 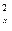 + m
+ m 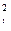 + m
+ m 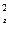 +…+ m
+…+ m 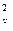 . (4.26)
. (4.26)
Если mX = mY = mZ = …=mU, а число измеренных величин X, Y, Z, …, U равно n, то
m 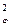 = nm2 или mφ = m√ n, (4.27)
= nm2 или mφ = m√ n, (4.27)
т. е. средняя квадратическая погрешность суммы равноточно измеренных величин в √n раз больше средней квадратической погрешности отдельного измерения.
П р и м е р. Найти среднюю квадратическую погрешность суммы измеренных углов в четырехугольнике, если средняя квадратическая погрешность одного угла равна ±30''. По формуле (4.27) находим
__
mφ = ± 30'' √ 4 = ±60'' = 1'.
Дата добавления: 2015-01-19; просмотров: 1272;
