Понятия об уравнивании геодезических измерений

Геодезические измерения характерны тем, что их всегда больше, чем необходимо для определения величин. Например, для решения треугольника измеряют три угла, тогда как было бы достаточно измерить два угла. Эти избыточные измерения выполняют с целью контроля и повышения точности определяемых величин. Результаты избыточных измерений вследствие погрешностей не могут точно удовлетворять математическим зависимостям между элементами геометрических фигур, к которым они относятся. Поэтому возникает необходимость в нахождении системы поправок к измеренным величинам, которая удовлетворяла бы геометрическим условиям. Однако таких систем может быть бесчисленное множество. Например, если сумма трех углов в треугольнике не равна 180^о, то можно предложить множество вариантов введения поправок в углы.

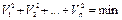В теории вероятности доказывается, что оптимальной (вероятнейшей) системой поправок является та, которая определяется под условием, чтобы сумма квадратов поправок в измеренные величины была минимальной, то есть или

[V ²] = min, (4.53)

где V – поправки к измеренным величинам.

Способ нахождения вероятнейших значения измеренных величин при наличии избыточных измерений под условием (4.53) называется методом наименьших квадратов. Совокупность вычисленных работ по нахождению наиболее надежных (вероятнейших) результатов по методу наименьших квадратов называется уравниванием. Уравнивание имеет две цели:

1) найти наиболее надежное значение неизвестных с оценкой точности полученных результатов;

2) исключить все математические противоречия в зависимостях, существующих между измеряемыми величинами.

В качестве примера применения метода наименьших квадратов покажем, что арифметическая середина является вероятнейшим значением измеряемой величины в равноточных измерениях.

Запишем условие (4.53) в виде

f(L) = V₁² + V₂² + … + V_n² = (l₁ – L)² + (l₂ – L)² + … + (l_n – L)² = min.

Из математики известно, что минимум функции будет, если первая производная ее равна нулю, а вторая – больше нуля, т. е.

f ^'(L) = – 2(l₁ – L) – 2(l₂ – L) – … – 2(l_n – L ) = 0; (4.54)

f ^''(L) = 2n > 0.

Решив уравнение, (4.54) относительно L, получим

nL = l₁ + l₂ + … + l_n,

откуда

L = (l₁ + l₂ + … + l_n) / n = [l] / n,

т. е. получим тот же результат, как и в формуле (4.4), что и обеспечивает метод наименьших квадратов.