РАСЧЕТЫ СТЕРЖНЯ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПРИ

РАСТЯЖЕНИИ (СЖАТИИ)

Центральным растяжением (сжатием) называется такой вид нагружения бруса, при котором внешние нагрузки или их равно­действующие приложены вдоль оси бруса. Брус с прямолинейной осью, работающий в условиях центрального растяжения (сжатия), называется стержнем. В поперечных сечениях стержня возникает один внутренний силовой фактор (ВСФ) - нормальная сила N_z . Для определения нормаль­ной силы используется метод сечения. Нормальная сила N_z в поперечном сечении равна сумме проекций всех сил, расположенных по одну сторону от этого сечения, на ось стержня. Нормальная сила N_z принимается положительной и направляется от сечения, если она вызывает растяжение. Величина нормальной силы в произвольном поперечном сечении стержня определяется по формуле:

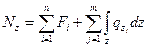(1)

где 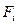- сосредоточенные силы, 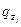- распределенные нагрузки.

Нормальное напряжение в произвольном поперечном сечении стержня вычисляется по соотношению:

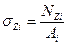(2)

где 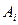- площадь поперечного сечения i - участка стержня.

При расчетах стержней на прочность находится опасное сечение, в котором напряжение достигает наибольших значений по абсолютной величине 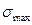, и для этого сечения записывается условие прочности:

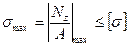(3)

где 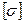- допускаемое нормальное напряжение для материала стержня. Для пластичных материалов - 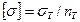, для хрупких материалов - 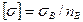, где 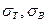- предел текучести и предел прочности материала стержня, 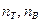- коэффициенты запаса прочности по пределу текучести и пределу прочности. Назначение величины коэффициента запаса прочности зависит от условий эксплуатации и области применения рассчитываемой конструкции, от методов расчета напряжений, свойств материала. Для пластичных материалов n_т принимается меньшим, чем n_в в случае расчета детали из хрупкого материала. Это обусловлено тем, что хрупкий материал более чувствителен к наличию различных дефектов структуры материала и возможным перегрузкам в процессе эксплуатации.

Перемещение рассматриваемого сечения стержня A§i, в соответствии с законом Р. Гука, вычисляется по формуле:

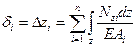. (4)

Произведение EA_i - в формуле (4) называется жесткостью сечения стержня при растяжении (сжатии).

По результатам вычислений нормальной силы N_z , нормального напряжения а и перемещений 5 строятся эпюры. Эпюра - это график, который показывает изменение силового фактора, напряжения, перемеще­ния и других величин по длине бруса (стержня).

В ряде случаев для обеспечения надежной работы стержня необхо­димо выполнение условия жесткости:

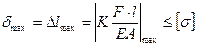(5)

где 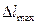- наибольшее абсолютное удлинение стержня, к - коэффициент, определяемый из эпюры перемещений, 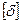- допускаемое удлинение стер­жня, зависящее от назначения и области применения конструкции.

ВАРИАНТЫ РАСЧЕТНО - ПРОЕКТИРОВОЧНОЙ РАБОТЫ

Вариант А

Расчет статически определимого стержня на прочность и жесткость при

растяжении (сжатии) Задаются:схема нагружения стержня (рис. 6), величины внешних нагрузок, размеры стержня, коэффициент запаса прочности пт (таблица 1).

При расчетах принять: 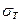=300МПа, q=200KH/M, P=0,5q/=50KH, Е=2·10⁵ Мпа, l=0,5м, 1МПа=10⁶Па=1Н/мм²=10⁶Н/м².

Требуется:1)Построить эпюры нормальных сил N_z, нормальных напряжений 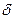и перемещений ;

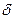2) из условия прочности определить размеры поперечных сечений стержня;

3) выполнить эскиз стержня в соответствии с заданными соотношениями.

4) реализовать машинный вариант выполнения РПР.

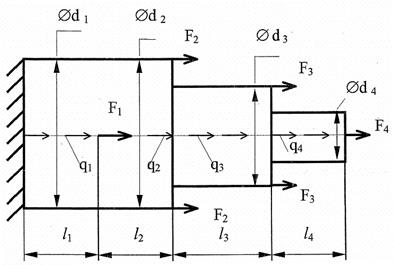
Рис.1. Обобщенная расчетная схема стержня.

Таблица 1

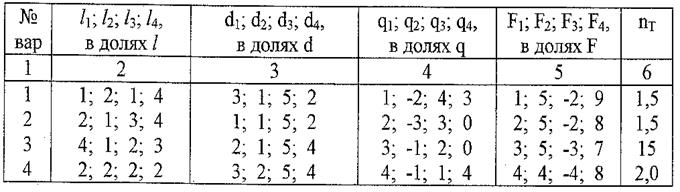
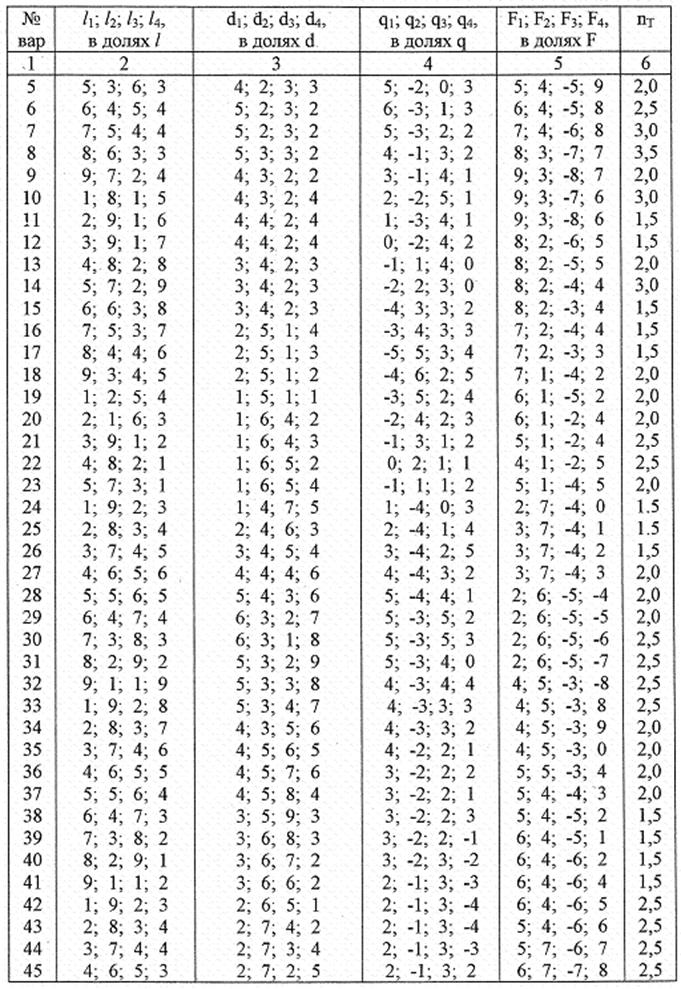
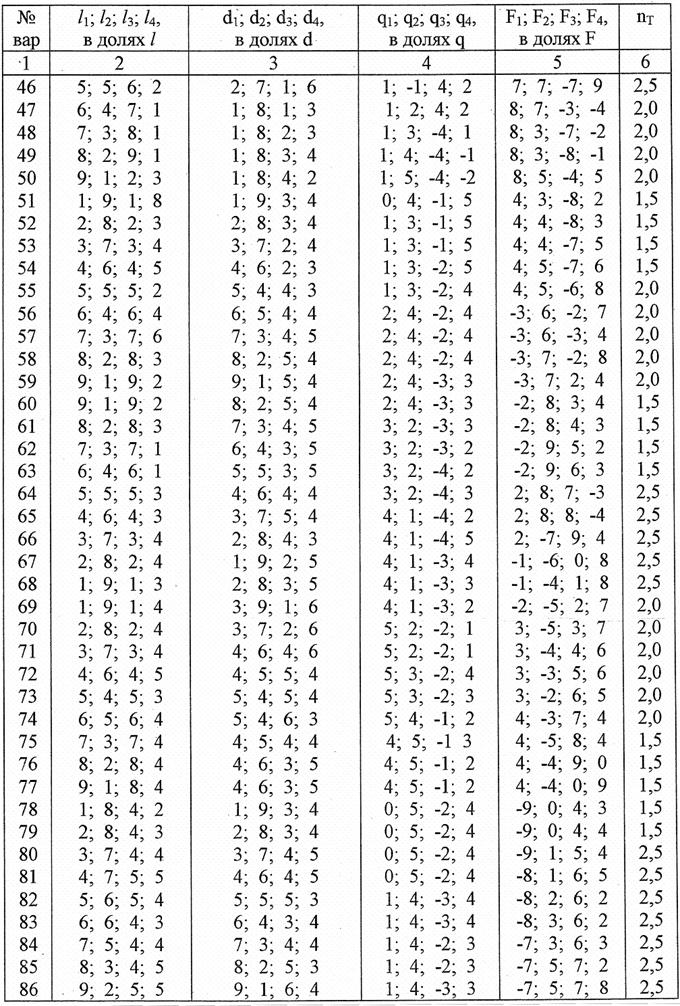
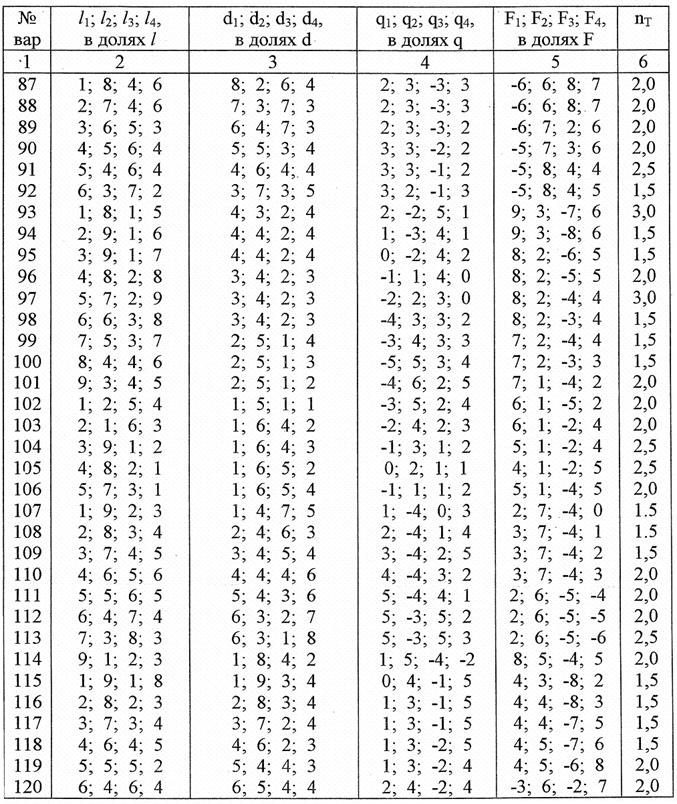
Вариант Б

Для ступенчатого стержня в соответствии с заданным вариантом требуется:

1) построить эпюру продольных усилий N_z;

2) из условия прочности подобрать размеры, 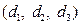сечений;

3) построить эпюру нормальных напряжений 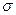в МПа;

4) построить эпюру осевых перемещений поперечных сечений по длине стержня;

5) из условия прочности на срез 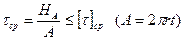и смятие

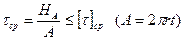определить необходимую толщину t и диаметр D

головки стержня;

6) выполнить эскиз стержня в соответствии с назначенными размерами.

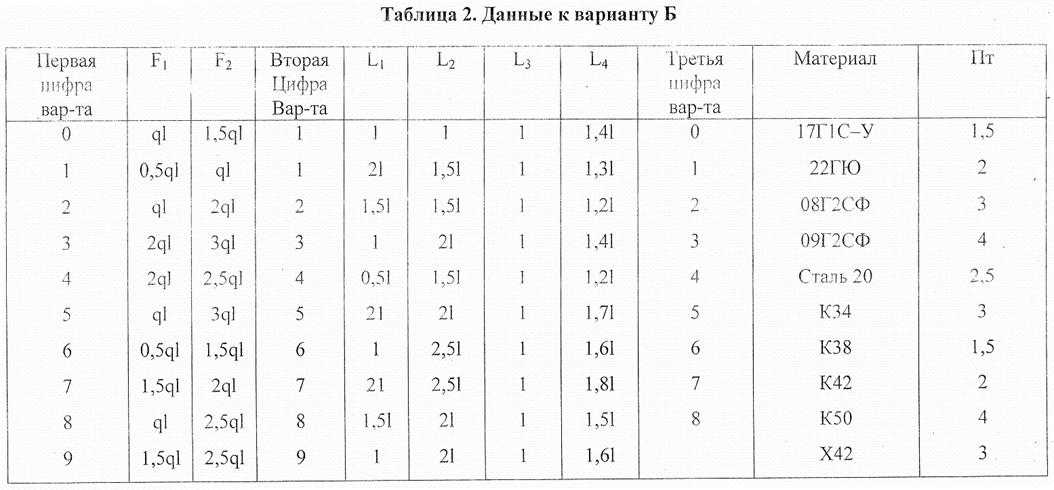
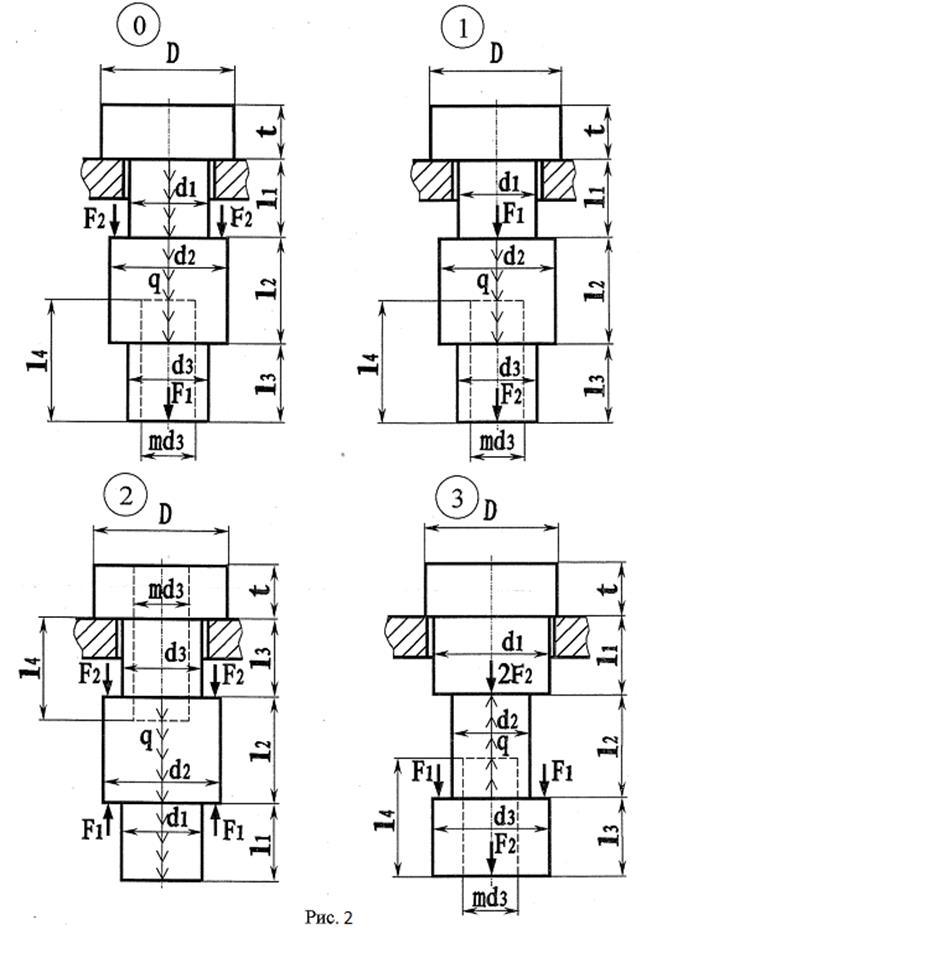
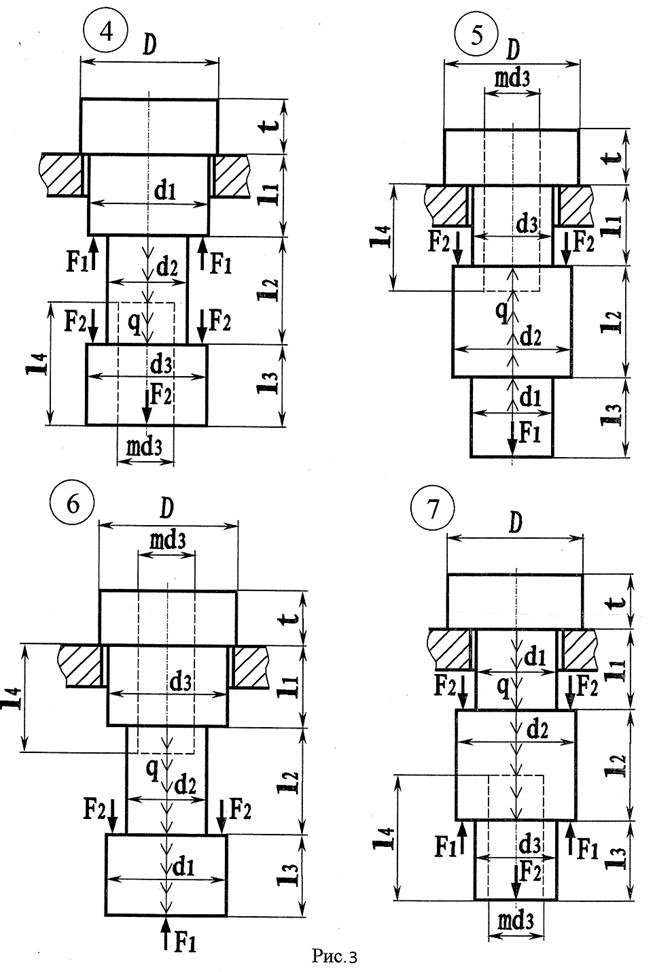
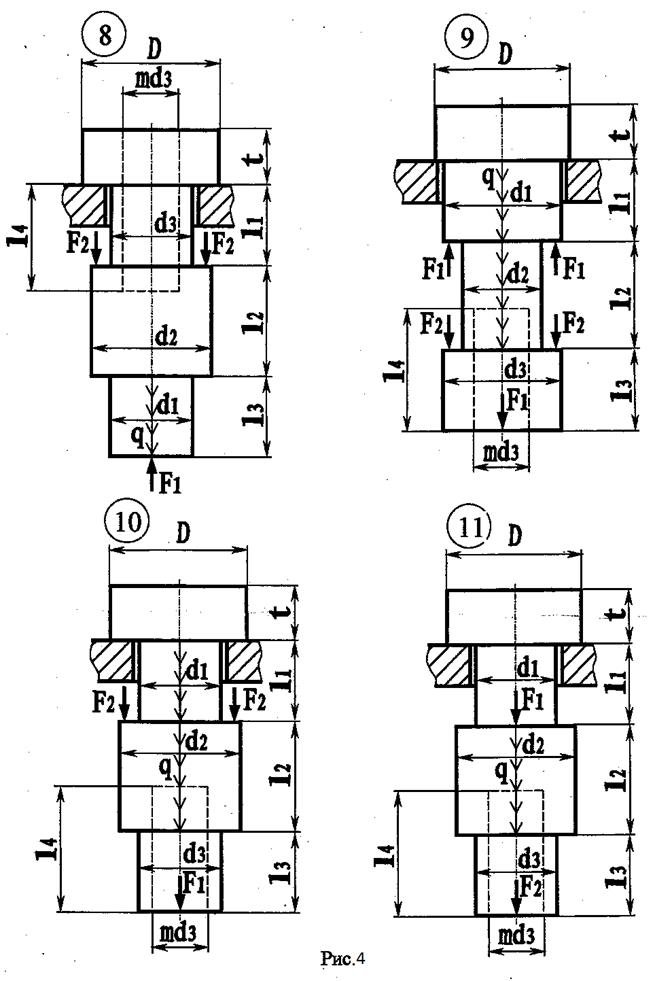
Последняя цифра варианта соответствует номеру схемы (рис. 2..4). Данные варианты даны в таблице 2.

В расчетах принять:

q=200 кН/ м; 1=0,1 м; Е=2·10⁵ МПа; [σ]_см=2[σ]р; [τ]_ср=(0,5...0,6) [σ]р.