Пример выполнения расчетно-проектировочной работы

Расчёт статически-определимого стержня на

прочность и жёсткость

Задаётся:схема нагружения стержня (рис.5,а), длины участков стержня: 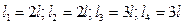, размеры поперечных сечений: d₁= 4d; d₂= 4d; d₃=3d; d₄=2d, величины распределённых нагрузок: q₁=2q; q₂=0; q₃=-4q; q₄=q, величины сосредоточенных сил: F₁= -2F; F₂= -4F; F₃=F; F₄=5F, предел текучести материала 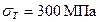, коэффициент запаса прочности n_т=2,0, q=200 кH/м, l=0,5м, F=0,5ql=50кH, Е=2·10⁵ МПа. При расчетах учитывать соотношения: 1МПа=10⁶Па=1Н/мм²=10²Н/см²=10⁶Н/м².

Требуется:1) Построить эпюры нормальной силы N_z , нормального напряжения 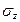и перемещения 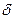; 2) из условия прочности определить размеры поперечных сечений стержня.

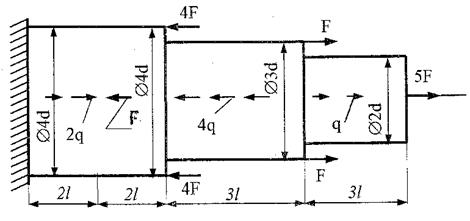
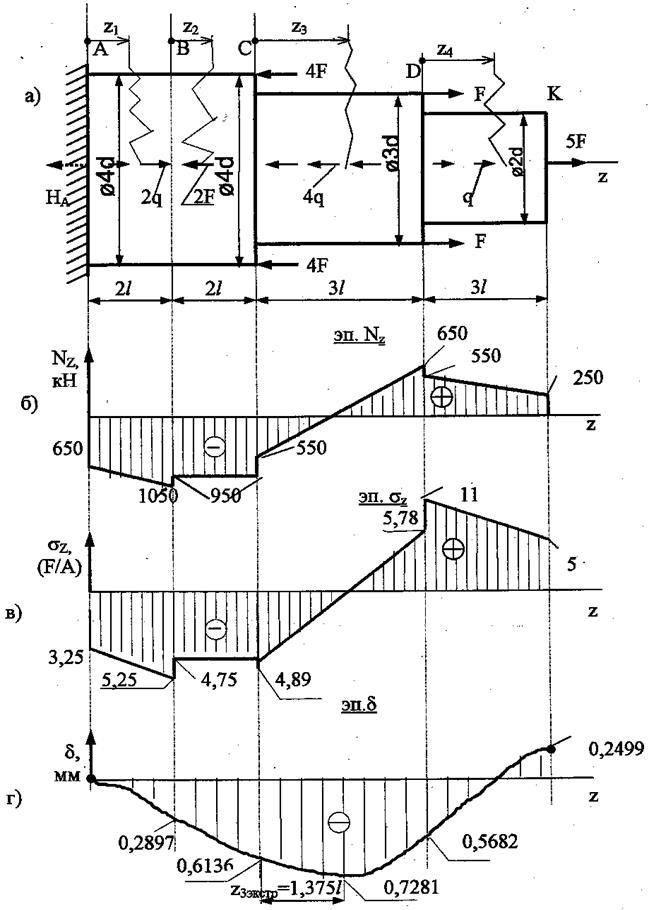
Рис.5. Расчетная схема стержня, эпюры нормальной силы, нормального напряжения и перемещений.

Решение

1. Определение опорной реакции Н_А в заделке (рис.5,а).

Для определения опорной реакции составляется уравнение равновесия стержня:

.

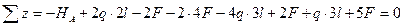Учитывая , что Р= 0,5ql определяется опорная реакция

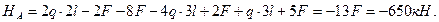
2. Разбивка стержня на участки.

Для построения эпюры нормальной силы N_z по длине стержня необходимо рассмотреть четыре участка с координатами z₁; z₂; z₃ и z₄ (рис.5,а).

3. Определение законов изменения нормальной силы по участкам стержня. Начало рассматриваемых участков необходимо обозначать точкой, текущее сечение z\ стрелкой. Начало последующего участка начинается на границе предыдущего участка.

3.1 Первый участок (рис.6)

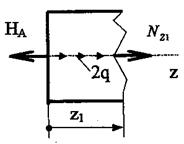
Рис.6 К определению 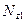на первом участке

Координата z₁ для первого участка изменяется в пределах 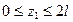. Уравнения равновесия для отсечённой (левой) части стержня имеет вид:

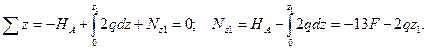
Нормальная сила на границах участка принимает значения:

при z₁=0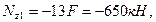

при z₁=2l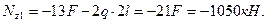

3.2 Второй участок (рис.7)

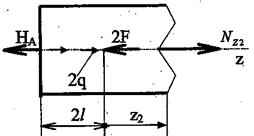
Рис 7. К определению N_z2 на втором участке

На втором участке координата z₂ изменяется в пределах 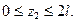Уравнение равновесия для отсечённой части стержня записывается в виде:

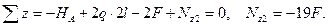
На втором участке нормальная сила постоянна по длине участка N_z2 = -19F.= -950кН

3.3 Третий участок (рис.8)

Координата z₃ на третьем участке изменяется в пределах 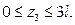Уравнение равновесия отсечённой части стержня и значения нормальной силы на границах участка соответственно равны:

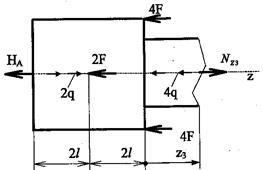
Рис.8 К определению N_z3 на третьем участке

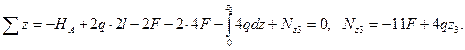
при z₃=0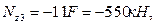

при z₃=3l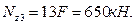

3.4 Четвёртый участок (рис.9)

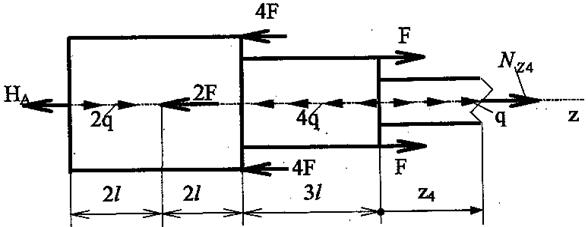
Рис.9 К определению N_z4 на четвертом участке

Координата z₄ на четвёртом участке изменяется в пределах 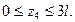Соответствующее уравнение равновесия отсечённой части стержня и значения нормальной силы на границах участка равны:

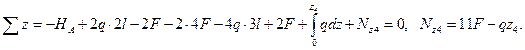
при z₄=0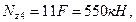

при z₄=3l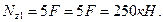

По результатам вычислений строится эпюра нормальных сил N_z (рис. 5,б).

4. Определение закона изменения нормального напряжения по участкам стержня.

Для определения нормального напряжения по участкам стержня предварительно вычисляются площади поперечных сечений:

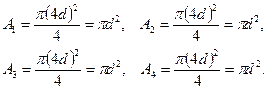
Затем наименьшее значение площади (в данном примере 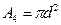) принимается за А ( 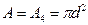) и определяются значения площадей поперечных сечений пропорционально A: A₁= 4A, А₂= 4А, А₃= 2,25А, А4=А.

4.1 На первом участке закон изменения нормального напряжения в соответствии с формулой (2) имеет вид:

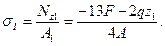
Нормальное напряжение на границах участка принимает значения:

при z₁=0;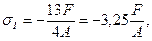

при z₁=2l;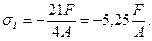

4.2 На втором участке закон изменения нормального напряжения имеет вид:

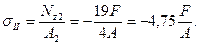
Нормальное напряжение на втором участке постоянно и равно

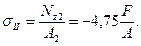
4.3 На третьем участке нормальное напряжение равно:

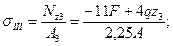
при z₃=0;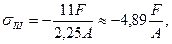

при z₃=3l;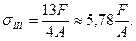

4.4 Нормальное напряжение на четвертом участке определяется по зависи-мости:

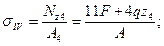
при z₄=0;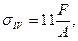

при z₄=3l;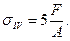

По результатам вычислений строится эпюра нормальных напряжений 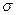(рис.5,в).

5. Выбор опасного сечения. Определение размеров поперечных сечений стержня.

Предварительно определяется допускаемое напряжение

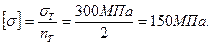Для данного примера опасным является

сечение, в котором действует наибольшее рабочее напряжение 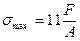(рис.5,в). Из условия прочности 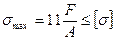определяются площадь и диаметр поперечного сечения в опасном сечении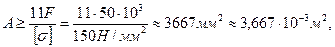

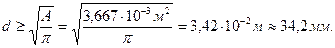
Площади поперечных сечений и диаметры по участкам стержня соответственно равны :

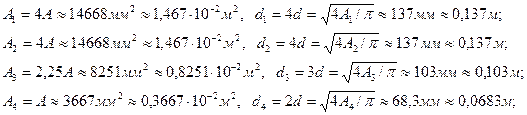
6. Определение перемещений на участках стержня.

6.1 Перемещение на первом участке, в соответствии с законом Р.Гука, равно

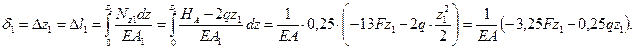
В координатах 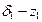полученное выражение описывает кривую второго порядка. Определим выпуклость кривой: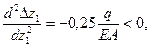

следовательно кривая 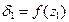выпукла вверх.

При 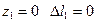, при

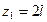
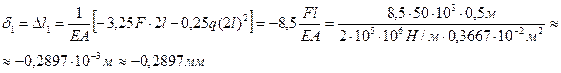
Условие экстремума кривой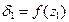

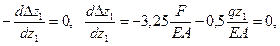следовательно функция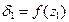

имеет экстремум за пределами ( 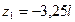) первого участка.

6.2 Перемещение на втором участке соответствует перемещению сечения В на первом участке плюс абсолютное удлинение сечения 2 по линейной зависимости

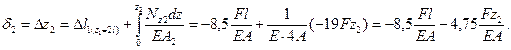
при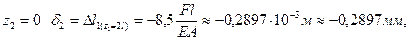

при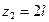

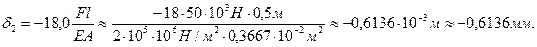
6.3. Перемещение на третьем участке соответствует перемещению сечения С на втором участке плюс абсолютное удлинение сечения 3 по кривой второго порядка

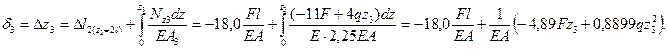
Определим выпуклость кривой: 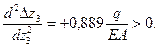Следовательно, кривая 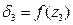выпукла вниз.

При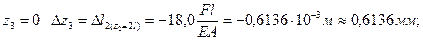

при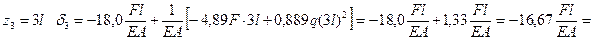

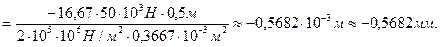
Условие экстремума кривой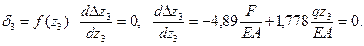

Следовательно функция 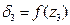имеет экстремум при 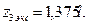Вычислим перемещение сечения при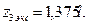

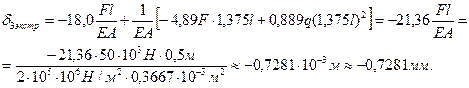
6.4. Перемещение на четвёртом участке соответствует перемещению сечения Д на третьем участке плюс абсолютное удлинение сечения 4 по кривой второго порядка

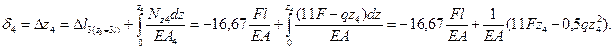
Определим выпуклость кривой: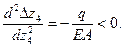

Следовательно кривая 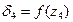выпукла вверх.

При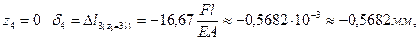

при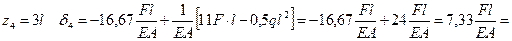

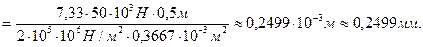
Условия экстремума кривой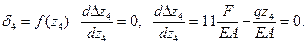

Следовательно функция 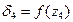имеет экстремум за пределами

(z₄ = 5,5l) четвёртого участка. По результатам вычислений строится

эпюра перемещений 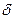(рис. 5.г).

7. В классе ПЭВМ кафедры студент реализует машинный вариант выполнения РПР, сопоставляет результаты традиционного и машинного расчетов.