РАСЧЕТЫ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СТЕРЖНЕЙ И СТЕРЖНЕВЫХ СИСТЕМ НА ПРОЧНОСТЬ И ЖЁСКОСТЬ

Статически неопределимыми называются такие стержни и стержневые системы, в которых реактивные факторы и внутренние усилия не могут быть определены только из уравнений равновесия. Данные системы классифици­руются по степени статической неопределимости. Степень статической не­определимости представляет собой разность между числом неизвестных реакций и числом уравнений равновесия. Степень статической неопредели­мости системы определяет количество дополнительных уравнений (уравне­ния перемещений), которые необходимо составить при раскрытии статической неопределимости.

В статически определимых стержневых системах усилия возникают только от действия внешней нагрузки. В статически неопределимых стерж­невых системах усилия возникают не только от внешних нагрузок, но и в ре­зультате неточности изготовления отдельных элементов системы, изменения температуры элементов системы и т.д. При отклонении действительных про­дольных размеров стержней от номинальных (расчётных) при сборке стати­чески неопределимых систем возникают дополнительные, так называемые монтажные усилия и напряжения. При изменении температуры статически неопределимой стержневой системы в ее элементах возникают дополнитель­ные, так называемые температурные усилия и напряжения.

Расчет статически неопределимых стержней и стержневых систем вы­полняется по следующей методике.

1. Проводится анализ схемы закрепления и определяется степень статиче­ской неопределимости стержневой системы.

2. Рассматривается статическая сторона задачи, т.е. составляются уравне­ния равновесия.

3. Анализируется геометрическая сторона задачи. Система рассматрива­ется в деформированном состоянии, устанавливается взаимосвязь между де­формациями или перемещениями отдельных элементов системы. Полученные уравнения являются уравнениями совместности перемещений (деформаций). Количество уравнений совместности перемещений (деформа­ции) равно степени статической неопределимости системы.

4. Рассматривается физическая сторона задачи. На основе закона Р.Гука перемещения или деформации элементов системы выражаются через дейст­вующие в них внутренние усилия и с учётом этого записываются уравнения совместности перемещений в развёрнутом виде.

5. Решая совместно уравнения равновесия и совместности перемещений в развёрнутом виде определяются неизвестные реакции, т.е. раскрывается ста­тическая неопределимость стержневой системы.

6. Дальнейший расчёт на прочность и жёсткость аналогичен расчёту статически определимых систем.

Методика решения статически неопределимых стержней и стержневых систем показана на примерах решения различных задач.

Пример 1.Ступенчатый стержень, защемлённый с обеих сторон, нагружен силами F (рис.10,а). Требуется раскрыть статическую неопределимость стержня и определить площадь поперечного сечения.

Исходные данные: длина участка стержня l, площадь поперечного сечения стержня А модуль продольной упругости материала стержня Е, допускаемое напряжение .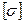

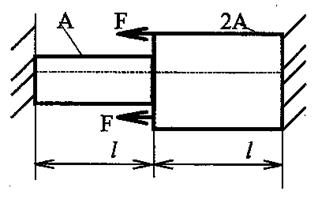
Заданная стержневая система.

Решение.

1. В результате действия внешних сил на стержень возникают две опорные реакции R₁ и R₂. Уравнений равновесия для плоской стержневой системы можно составить одно 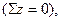следовательно стержень один раз статически неопределим (рис. 10,6).

2. Рассматривается статическая сторона задачи. Выбирается расчётная схема (рис. 10,6) и составляется уравнение равновесия:

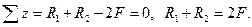
3. Анализируется условие деформирования стержня и геометрическая сторона задачи, составляется уравнение совместности перемещений.

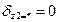
4. Рассматривается физическая сторона задачи. Условно принимая, что реакции R₁ и R₂ известны, определяются нормальные силы на участках

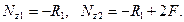
На основе закона Р.Гука записываются выражения перемещений на каждом участке, и затем составляется уравнение совместности перемещений в развёрнутом виде:

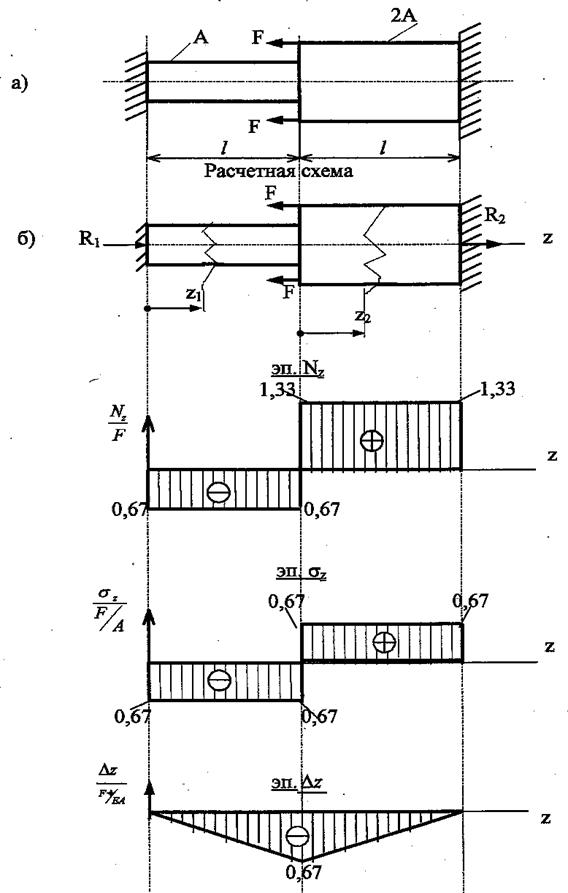
Рис.10. Заданный стержень, расчетная схема стержня, эпюры нормальной силы, нормального напряжения и перемещений

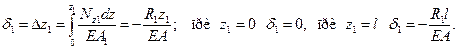
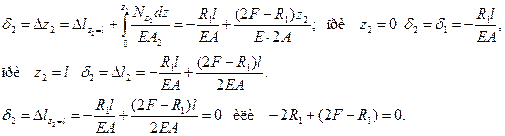
5. Совместное решение уравнения равновесия и уравнения совместности перемещений в развёрнутом виде позволяет определить неизвестные реакции 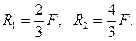Статическая неопределимость стержня раскрыта.

6. Строятся эпюры N_z, σ_z, δ (рис 10). Записывается условие прочности

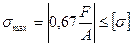и определяется площадь поперечного сечения стержня

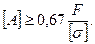
Пример 2. Абсолютно жёсткий брус шарнирно крепится к стержням и опирается на шарнирно неподвижную опору (рис. 11,а). К брусу приложена сила F. Требуется раскрыть статическую неопределимость стержневой системы и определить величину допускаемой силы [F].

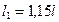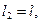Исходные данные: длины стержней и длины участков бруса заданы в долях а, площади поперечного сечения стержней A₁= 2A и A₂=А, модуль упругости материала стержней Е, допускаемое напряжение .

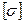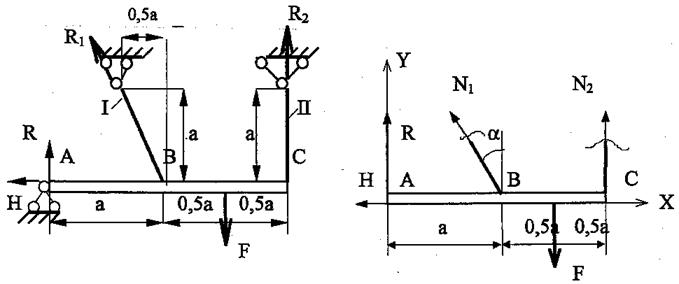
Рис.11,а Рис. 11,б

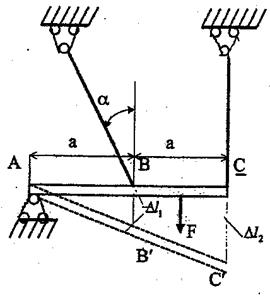
Рис. 11, в

Решение.

1. Заданная стержневая система один раз статически неопределима, поскольку неизвестных реакций четыре - Н, R, R₁, R₂, а уравнений равновесия для плоской системы сил - три.

2. Рассматривается статическая сторона задачи (рис. 11,6). Составляются уравнения равновесия

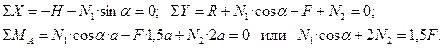
3. Анализируется геометрическая сторона задачи (рис. 11,в) и составляется уравнение совместности перемещений. Из подобия треугольников 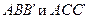имеем:

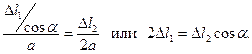
4. Рассматривается физическая сторона задачи. На основе закона Р.Гука определяются выражения деформаций 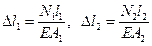, и затем записывается уравнение совместности перемещений в развёрнутом виде:

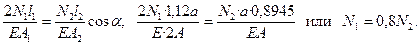
5. Совместное решение уравнений равновесия и развёрнутого уравнения совместности перемещений позволяет определить величины усилий в стержнях через внешнюю нагрузку N₁ =0,442P, N₂ = 0,552Р. Статическая неопределимость системы раскрыта.

6. Определяется допускаемая нагрузка [F].

Из условия прочности I стержня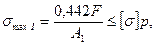

допускаемая нагрузка равна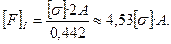

Из условия прочности II стержня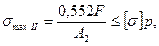

допускаемая нагрузка равна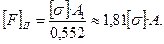

Окончательно принимаем для стержневой системы меньшее значение 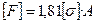. При этом рабочие напряжения во II стержне будут равны допускаемым, а первый стержень будет недогружен.

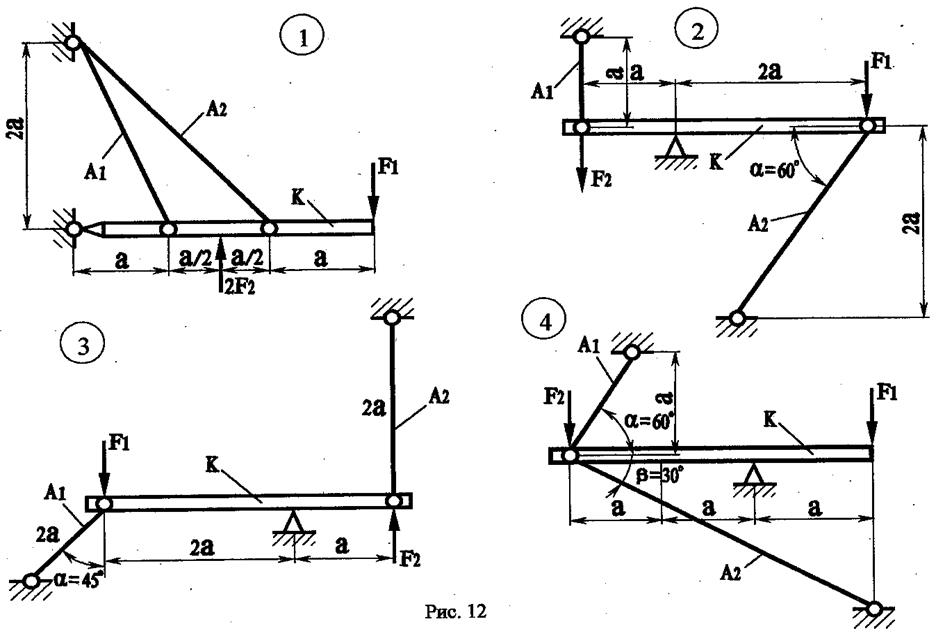
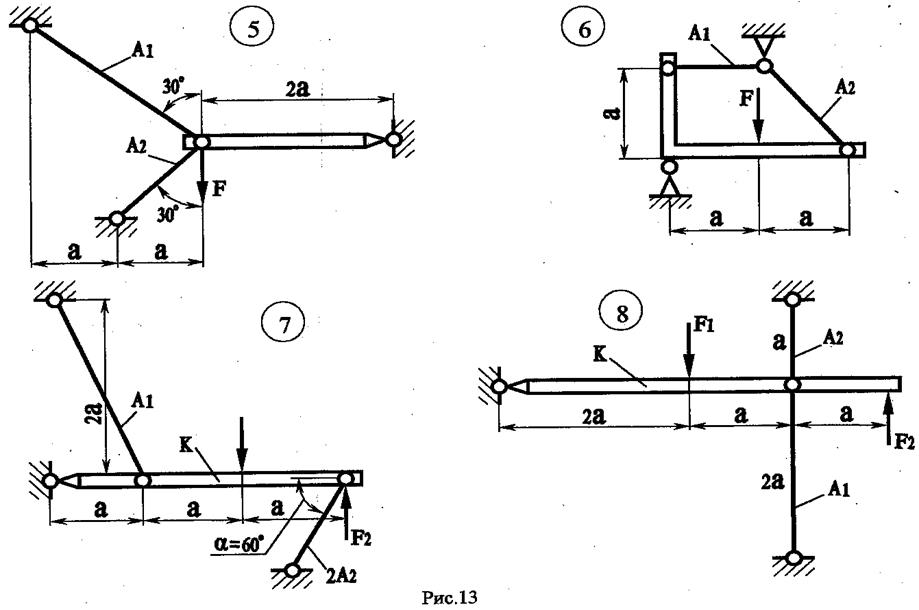
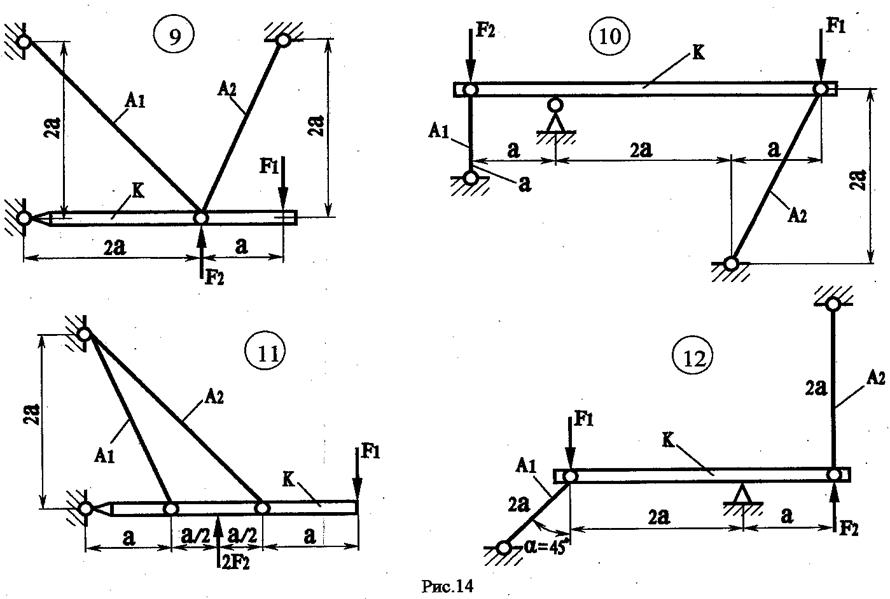
ВАРИАНТЫ РАСЧЕТНО - ПРОЕКТИРОВОЧНОЙ РАБОТЫ

РАСЧЕТЫ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СТЕРЖНЕЙ И СТЕРЖНЕВЫХ СИСТЕМ НА ПРОЧНОСТЬ И ЖЕСТ­КОСТЬ ПРИ РАСТЯЖЕНИИ (СЖАТИИ)

Абсолютно жесткий брус К, нагруженный силами F;, удерживается в равновесии стальными стержнями длиной щ и крепится посредством опор­ных устройств. Требуется выполнить проектировочный расчет (найти пло­щади поперечных сечений стержней).

Последняя цифра соответствует номеру схемы (рис. 12... 14).

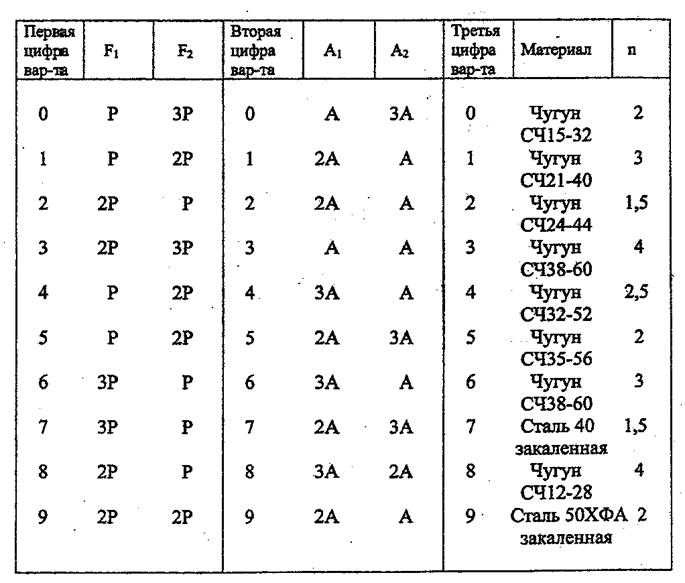
Данные варианта приведены в таблице 3.

В расчетах принять: Р =10 кН.

Таблица 3. Данные к задаче РПР