Теоретична частина. Електричним струмом називається будь-який впорядкований (спрямований) рух електричних зарядів

Електричним струмом називається будь-який впорядкований (спрямований) рух електричних зарядів. У провіднику під дією прикладеного електричного поля 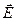вільні електричні заряди переміщуються: позитивні по полю, негативні – проти поля, тобто в провіднику виникає електричний струм, який називається струмом провідності. Для виникнення і існування електричного струму необхідно: 1) наявність вільних носіїв струму – заряджених частинок, здатних переміщуватися впорядковано; 2) наявність електричного поля, енергія якого, поповнюючись, витрачається на впорядкований рух.

Узагальнений закон Ома для неоднорідної ділянки кола представляється виразом

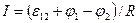, (9.1)

де I – струм на ділянці кола 1-2, ε₁₂ – ЕРС, що діє на цій ділянці, φ₁-φ₂ – різниця потенціалів кінців ділянки, R – опір ділянки кола. Якщо на даній ділянці кола джерело струму відсутнє (ε₁₂ = 0), то приходимо до закону Ома для однорідної ділянки кола:

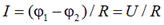(9.2)

Якщо коло замкнене, тобто точки 1 і 2 співпадають (φ₁=φ₂), отримуємо закон Ома для замкненого кола:

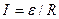, (9.3)

де ε – ЕРС, що діє в колі, R – сумарний опір всього кола. R = r + R₁, r – внутрішній опір джерела струму, R₁ – опір зовнішнього кола.

Для розрахунку розгалуженого кола, що містить декілька замкнених контурів (контури можуть мати спільні ділянки, кожен з них може мати кілька джерел струму і т. д.) використовують правила Кирхгофа.

Будь-яка точка розгалуження кола, в якій сходиться не менше трьох провідників із струмом, називається вузлом. Струм, що входить у вузол, вважається позитивним, а струм, який виходить з вузла, – негативним. Перше правило Кирхгофа: алгебраїчна сума струмів, що сходяться у вузлі, дорівнює нулю:

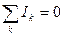. (9.4)

Друге правило Кирхгофа: у будь-якому замкненому контурі, вибраному в розгалуженому електричному колі, алгебраїчна сума добутків сили струму I_k і опору R_k , що відповідають ділянці контуру між двома вузлами, дорівнює алгебраїчній сумі ЕРС ε_k , що діють в цьому контурі:

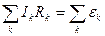. (9.5)

Для визначення опорів в роботі використовують місток Уітстона (рис. 9.1), де R_x – невідомий опір, R – магазин опорів, ADB – рео-

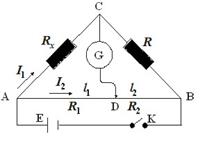
хорд.

Рисунок 9.1

Містком є галузь СD, що містить гальванометр G. Якщо замкнути ключ К, струм від джерела Е буде йти по розгалуженому колу і містку СD. Змінюючи опір магазину, можна досягти того, щоб по містку СD струм не йшов. В цьому випадку потенціали точок С і D будуть однакові. Однаковими будуть також і різності потенціалів між точками А і С, А і D. Із закону Ома (9.2) випливає

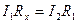, (9.6)

де І₁ та І₂ – сила струму на ділянках АС і АD, відповідно.

Аналогічно, з однаковості різності потенціалів між точками С і В, D і В випливає, що

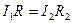. (9.7)

Поділивши (9.6) на (9.7), отримуємо

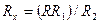, (9.8)

де R₁ і R₂ – опори ділянок дроту реохорду зліва і справа від його движка (ковзаючого контакту).

Опір дроту знаходиться за формулами

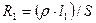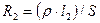, , (9.9)

де ρ – питомий опір матеріалу дроту, S – площина його перетину, l₁ і l₂ – довжини плечей реохорду (відстань від кінців реохорду до його движка). Тоді з формул (9.8), (9.9) знаходимо, що

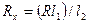. (9.10)