Theoretical part. 1. The ordered motion of electric charges is called the electric current
1. The ordered motion of electric charges is called the electric current. An electric current in metals is the motion of the conductivity electrons. In conducting solutions (electrolytes) ions are the mobile charges. The ions and the electrons carry charges in gases.
Intensity and density are the quantative characteristics of the electrical current. Intensity of current is the charge dq passesthrough a cross section of a conductor in a time dt:
 .
.
If the same amount of electric charges flows through any section of conductor at the equal period of time, the current intensity is constant value I= dq/dt = const. If the current changes by time, it is alternating current dq/dt≠const. The intensity of current is a scalar value and measured in amperes in the SI system. Current intensity is measured in milliamperes (mA) and microamperes (μA) too.
If current is assigned irregularly along the surface S, then the current density j is defined in every point of the surface. The current density is the ratio
 ,
,
where dS is an area perpendicular to the current direction dI which goes through this area.
The current intensity I through the given surface S can be found with the help of integration:
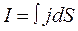 .
.
If the current I is assigned regularly through the given surface S then the current density-j=I/S=const. The current density is a vector value and inSI system measured in amperes divided by square meter(A/m2).
The density of a charge j can be assigned by concentration of the charges, it’s value and velocity
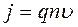 .
.
2. There is relationship between the voltage U applied to the ends of the conductor and the current in it for each conductor if the condition of the conductor is invariable:
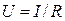 .(8.1)
.(8.1)
It’s the Ohm’s law for the part of the electric circuit in integral form. According to the Ohm’s law in the differential form j=σE the current density j in the conductor is directly proportionate to the electric intensity E in it, where σ is specific electroconductivity of the conductor. The Ohm’s law for the closed circuit is
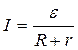 ,
,
where ε - electromotive force,
R - external resistance of the conductor,
r - internal resistance of current source.
When the current passes through the conductor, the latter is being heated. The quantity of the produced heat in the conductor is proportionate to its resistance, square value of current intensity and time:
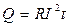 . (8.2)
. (8.2)
If the current intensity changes in time, then:
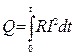 . (8.3)
. (8.3)
The formulas (8.2) and (8.3) represent the Joule-Lenz’ law. The heat quantity Q, which turns from the volume unit into the time unit of the conductor, is called the power of the current. The Joule-Lenz’ law in differential form is:
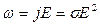 .
.
3. Simple electric circuits are closed loops. The calculation of the ramified electric circuit is more complex but significantly simplified if we use Kirchhoff’s laws.
The first law deals with the junction points and states: the algebraic sum of the currents at any junction point equals to zero (Fig. 8.1). For the junction point A:
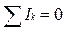
or -I1-I2+I3=0.
The second law deals with electric circuits: for any closed loop the algebraic sum of all incidences of voltage IiRi is equal to the algebraic sum of all the electromotive forces εi in this circuit.
For the 1 circuit
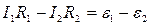 .
.

Figure 8.1
For the 2 circuit
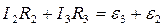 .
.
4. The conductor’s resistance is directly proportional to its length and inversely proportional to its cross-section area
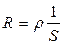 , (8.4)
, (8.4)
where ρ- the specific resistance of the conductor,
l - the length of the conductor,
S - cross-section area.
The conductors in the electric field can be connected in series and parallel.
When the conductors connected in series the current has the same value of I (fig. 8.2).
Voltage drop in each resistance
 ;
; 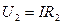 ;
; 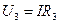 .
.
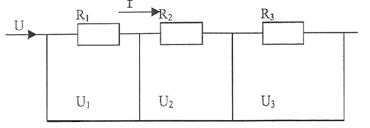
Figure 8.2
Adding right and left parts of these equations we obtain:
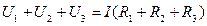 .
.
Hence it follows, that for any n amount of resistances connected in series there is a common resistance:
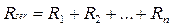 .(8.5)
.(8.5)
In case of parallel resistance the common current I is branched into 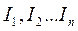 currents.
currents.
Let us consider parallel connection for three conductors (fig. 8.3):
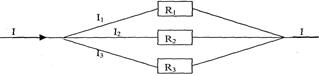
Figure 8.3
Voltage drop in each resistance is the same:
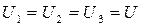 ;
;
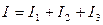 ;
; 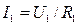 ;
; 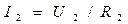 ;
; 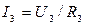 ;
; 
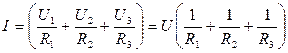 .
.
In general for n amount of the conductors connected in parallel the total resistance may be expressed by the formula
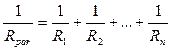 .
.
Дата добавления: 2015-03-20; просмотров: 1234;
