Theoretical part

An electrostatic field is created by immobile charges and determined in each point of space by the force acting on a test charge.

The main characteristic of an electrostatic field is the intensity

, (11.1)

where 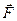is the force acting on a point charge q placed into the point under consideration.

An energetic characteristic of an electrostatic field is the electrostatic potential U. It is measured by the work that is performed by an electric force when a unit positive charge is shifted from this point to the infinity.

When a charge shifts from arbitrary point 1 to arbitrary point 2, the work performed is independent of a trajectory and due to a difference of potentials:

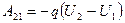. (11.2)

Potential is a function of coordinates 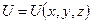. If a potential distribution is known, an intensity can be found being

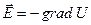, (11.3)

where operator grad in the right side is called the gradient. It acts on scalar function of coordinates by the rule

. (11.4)

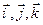are unit vectors along axis x, y and z respectively.

An electrostatic field can be represented with equipotential surfaces (equipotential lines in two-dimensional case). The equipotential surface (line) is a locus of points with equal potential.

To represent an electrostatic field lines of force (lines of intensity) can be also used. The line of force is a line with tangent at each point coinciding with vector of intensity. Constructing lines of force, one can use their properties:

a) lines of force start from positive charges and finish at negative ones (or disperse in infinity);

b) crossing equipotential surfaces (lines), lines of force are directed perpendicularly to them;

c) lines of force come out (or come in) perpendicularly to electrodes since charged metallic surfaces are equipotential;

d) lines of force are concentrated in the places where intensity is higher;

e) lines of force are directed down in potential.

There is an analogy between of an electrostatic potential distribution in a homogeneous dielectric medium and a potential distribution in a homogeneous conductor with an electric current. It can be explained by the fact that both cases are described by the same equation which doesn't include any parameter of a medium

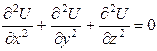. (11.5)

This equation can be applied to a dielectric as well as to a conductor. It is possible to study an electrostatic field in a dielectric medium by measuring a distribution of potential in a conductor although this potential distribution is of different origin.