Обчислення дисперсії.
Дисперсія посідає особливо місце в статистичному аналізі соціально-економічних явищ і є важливим елементом статистичних методів зокрема у дисперсійному аналізі. Для ознак метричної шкали дисперсія є базою для обчислення середнього квадратичного відхилення 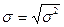 .
.
Дисперсія, на відміну від інших характеристик варіації є адитивною величиною. Тобто у структурованій сукупності, яка поділена на m груп за факторною ознакою х , загальна дисперсія 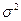 результативної ознаки у, може бути розкладена на: дисперсію у кожній групі (внутрішньогрупову) та дисперсію між групами (міжгрупову).
результативної ознаки у, може бути розкладена на: дисперсію у кожній групі (внутрішньогрупову) та дисперсію між групами (міжгрупову).
Загальна дисперсія характеризує варіацію ознаки у за рахунок впливу всіх причин(факторів), міжгрупова – за рахунок фактору х , покладеного в основу групування, а внутрішньогрупові – за рахунок інших факторів, не врахованих у групуванні.
Внутрішньо групова дисперсія розраховується окремо для кожної j-ї групи:
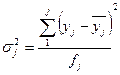 ,
,
де 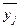 – середня j-ї групи;
– середня j-ї групи;
 – значення ознаки окремих елементів сукупності;
– значення ознаки окремих елементів сукупності;
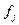 – чисельність одиниць (частота) j-ї групи;
– чисельність одиниць (частота) j-ї групи;
Для усіх груп в цілому розраховується середня з внутрішньогрупових дисперсій, зважених на частоти відповідної групи:
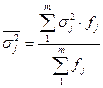 ,
,
де 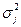 – внутрішньогрупова дисперсія j-ї групи.
– внутрішньогрупова дисперсія j-ї групи.
Міжгрупова дисперсія δ2 (дельта) розраховується за формулою:
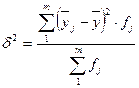 ,
,
де 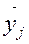 та
та 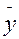 – відповідно середня j-ї групи та загальна середня варіюючої ознаки
– відповідно середня j-ї групи та загальна середня варіюючої ознаки 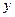
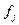 - чисельність одиниць (частота) j-ї групи.
- чисельність одиниць (частота) j-ї групи.
Взаємозв’язок між трьома дисперсіями дістав назву правила складання дисперсій, згідно яких:
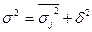 .
.
Користуючись цим правилом можна за двома відомими дисперсіями знайти третю – невідому, а також мати уяву про силу впливу групувальної ознаки.
В умовах широкого застосування обчислювано техніки, зокрема ПЕОМ, зручніше вести обчислення дисперсій за формулою різниці квадратів:


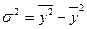 ,
,
де 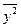 – середній квадрат значень варіюючої ознаки,
– середній квадрат значень варіюючої ознаки,
 – квадрат середньої величини.
– квадрат середньої величини.
Наведена формула дисперсії матиме такий вигляд для згрупованих даних^
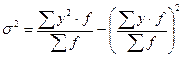 .
.
Розрахунок зазначених дисперсій показано за даними табл. 5.8 на прикладі депозитних процентних ставок в окремих відділеннях банків, %.
Таблиця 5.8 – Депозитні процентні ставки 10 відділень банків
| Відділення комерційних банків | Депозитні ставки в окремих відділеннях, % | |||||
| Центральні | – | – | ||||
| Філії |
По даним табл. 5.8 визначимо групові, міжгрупову та загальну дисперсію процентної ставки і покажемо окремо їх зв’язок.
Складаємо робочу таблицю:
| Відділення | Кількість відділень
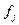
| Процентні ставки, % У | 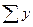
|  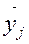
|
| Центральні | 16,22,20,18 | |||
| Філії | 25,31,33,28,27,24 | |||
| В цілому | Х | 24,4 |
Варіація депозитних процентних ставок для кожного відділення банку визначається двома внутрішньогруповими дисперсіями.
Для центральних відділень внутрішньогрупова дисперсія становить:
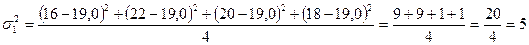 .
.
Для філій:
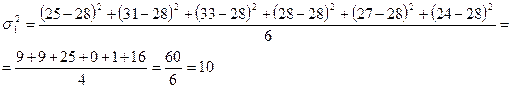
Середня з внутрішньогрупових дисперсій дорівнює
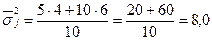
Для розрахунку міжгрупової дисперсії необхідно знати загальну середню варіюючої ознаки

Розрахунок міжгрупової дисперсії:
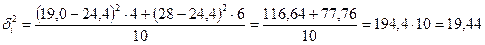 ,
,
де 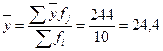
Загальна дисперсія як сума між групової та середньої з групових дисперсії:
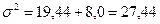 .
.
Безпосереднє обчислення загальної дисперсії за спрощеною формулою:
 .
.
Середнє квадратичне відхилення (зважене):
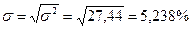 .
.
Квадратичний коефіцієнт варіації:
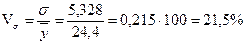 .
.
Таким чином, сукупність є однорідною, а середня – типовою, так як коефіцієнт варіації не перевищує 33%.
Дата добавления: 2015-03-20; просмотров: 7109;
