Теоретическое введение. При вращении тела вокруг закрепленной оси все его точки описывают окружности различного радиуса и, следовательно
При вращении тела вокруг закрепленной оси все его точки описывают окружности различного радиуса и, следовательно, имеют различные перемещения, скорости и ускорения. Тем не менее можно описать вращательное движение всех точек тела одинаковым образом. Для этого используют следующие кинематические характеристики движения: угол поворота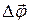 
, угловую скорость 
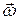и угловое ускорение 
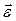. Эти характеристики будут одинаковы для любой точки абсолютно твердого тела. Модуль вектора поворота равен величине угла поворота Δφ; вектор поворота направлен по оси вращения по правилу буравчика (правого винта).
Угловая скорость тела 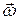характеризует быстроту вращения. Она равна отношению вектора элементарного угла поворота тела к продолжительности этого поворота:
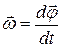. (8.1)
Быстроту изменения угловой скорости во времени характеризует угловое ускорение
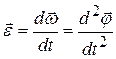. (8.2)
При возрастании угловой скорости ω угловое ускорение 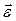совпадает с ней по направлению, при убывании – направлено в противоположную сторону.
Найдем связь между линейными и угловыми величинами. Величина линейного перемещения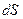 
точки, вращающейся по окружности радиуса 
:
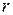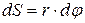. (8.3)
Разделив обе части уравнения (8.3) на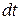 
, получим: 
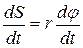. Так как производная пути по времени – это величина скорости: 
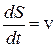, а 
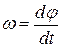(8.1), то:
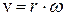. (8.4)
Теперь продифференцируем (8.4) по времени: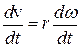 
, или:
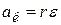, (8.5)
где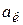 
– касательное (тангенциальное) ускорение, определяющее быстроту изменения модуля скорости 
:
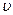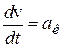. (8.6)
Динамика твердого тела.
Моментом силы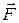 
относительно точки О называется физическая величина, равная векторному произведению радиус-вектора 
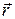, проведенного из точки О в точку приложения силы, на вектор силы :
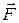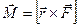. (8.7)
Направление момента силы определяется правилом буравчика (рис.8.1), величина момента силы
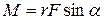, (8.8)
где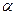 
– угол между радиус-вектором 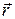точки приложения силы и вектором силы 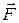. Момент силы относительно оси характеризует способность силы вращать тело вокруг этой оси. Составляющая силы, параллельная закреплённой оси, вращения тела вызвать не может, а напряжения, при этом возникающие в оси, нас не интересуют. Тогда достаточно рассмотреть силы, направления которых перпендикулярны оси вращения ОО’ (рис.8.1). Определим плечо силы 
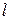относительно оси ОО’ как расстояние от оси вращения до линии действия силы, тогда
, 
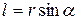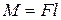. (8.9)
Более того, поворот тела с закрепленной осью вращения может быть вызван только касательной составляющей силы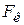 
, причем эта составляющая тем успешнее осуществит поворот, чем больше ее плечо r:
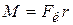, (8.10)
так как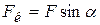 
.
Пусть твердое тело разбито на отдельные элементарные массы Δm. Выразим касательную составляющую равнодействующей сил, приложенных к этой точке, по второму закону Ньютона:
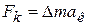. (8.11)
Учитывая (8.5) для касательного ускорения, получим из (8.10) и (8.11):
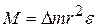. (8.12)
Скалярная величина
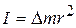, (8.13)
равная произведению массы материальной точки на квадрат ее расстояния до оси, называется моментом инерции материальной точки относительно оси.
Векторы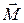 
и 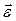совпадают по направлению с осью вращения, связаны с направлением вращения по правилу буравчика, поэтому равенство (8.12) можно переписать в векторной форме:
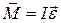. (8.14)
Уравнение (8.14) является основным законом динамики вращательного движения для материальной точки. Соотношение, аналогичное (8.12), можно записать для каждой точки тела, и затем просуммировать по всем точкам, тогда (с учетом того, что угловое ускорение одинаково для всех точек и его можно вынести за знак суммы):
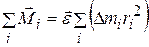. (8.15)
В левой части равенства стоит сумма моментов всех сил (и внешних, и внутренних), приложенных к каждой точке тела. Но по третьему закону Ньютона силы, с которыми точки тела взаимодействуют друг с другом (внутренние силы), равны по величине и противоположны по направлению и лежат на одной прямой, поэтому их моменты компенсируют друг друга. Таким образом, в левой части (8.15) остается суммарный момент только внешних сил.
Сумма произведений элементарных масс на квадрат их расстояний от оси вращения называется моментом инерции твердого тела относительно данной оси:
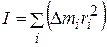. (8.16)
Моментинерции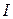 
твердого тела является мерой инертных свойств твердого тела при вращательном движении и аналогичен массе тела во втором законе Ньютона. Он зависит не только от массы тела, но и от ее распределения относительно оси (в направлении, перпендикулярном оси). В случае непрерывного распределения массы сумма в (8.16) сводится к интегралу по всему объему тела:
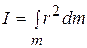. (8.17)
Моменты инерции для некоторых однородных тел относительно осей симметрии тел приведены в работе 1-07.
Таким образом, угловое ускорение твердого тела прямо пропорционально суммарному моменту внешних сил, приложенных к телу, и обратно пропорционально моменту инерции тела относительно оси вращения
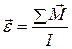. (8.18)
Это – основной закон динамики твердого тела. Он аналогичен второму закону Ньютона при поступательном движении
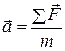(8.19)
и позволяет определить угловое ускорение твердого тела.
Подсчет момента инерции тела относительно произвольной оси облегчается применением теоремы Штейнера: момент инерции тела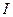 
относительно любой оси равен сумме момента инерции 
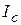относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния 
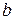между осями
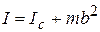. (8.20)
Экспериментальная часть
Приборы и оборудование: лабораторная установка, секундомер, штангенциркуль.
|
. Схема установки представлена на рис.8.2.
Крестовина состоит из четырех стержней 2, закрепленных под прямым углом к оси и друг к другу. На каждый стержень надето по одинаковому грузу 3, которые можно передвигать вдоль стержня и закреплять в любой точке между его основанием и концом. Масса каждого грузика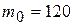 
г. На шкив 4 навита привязанная к нему одним концом нить 5, на другом конце которой подвешивается гиря 7 массы 
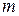. Нить перекинута через блок 6. В верхнем положении гиря удерживается вручную. Груз 7 освобождают, предоставляя ему возможность свободного падения. Измерения времени падения груза производятся при помощи секундомера, который включают и выключают в соответствующее время.
Дата добавления: 2015-03-19; просмотров: 533;